【题目】已知在数轴上,一动点![]() 从原点
从原点![]() 出发,沿直线以每秒钟
出发,沿直线以每秒钟![]() 个单位长度的速度来回移动,其移动方式是先向右移动
个单位长度的速度来回移动,其移动方式是先向右移动![]() 个单位长度,再向左移动
个单位长度,再向左移动![]() 个单位长度,又向右移动
个单位长度,又向右移动![]() 个单位长度,再向左移动
个单位长度,再向左移动![]() 个单位长度,又向右移动
个单位长度,又向右移动![]() 个单位长度…
个单位长度…
![]()
(1)求出![]() 秒钟后动点
秒钟后动点![]() 所处的位置;
所处的位置;
(2)如果在数轴上还有一个定点![]() ,且
,且![]() 与原点
与原点![]() 相距20个单位长度,问:动点
相距20个单位长度,问:动点![]() 从原点出发,可能与点
从原点出发,可能与点![]() 重合吗?若能,则第一次与点
重合吗?若能,则第一次与点![]() 重合需多长时间?若不能,请说明理由.
重合需多长时间?若不能,请说明理由.
参考答案:
【答案】(1)Q处于﹣2;(2)①当点A在原点左边时,时间=390秒(6.5分钟);②当点A原点左边时,时间=410秒 (6![]() 分钟).
分钟).
【解析】
(1)先根据路程=速度×时间求出5秒钟走过的路程,然后根据左减右加列式计算即可得解;
(2)分点A在原点左边与右边两种情况分别求出动点走过的路程,然后根据时间=路程÷速度计算即可得解.
解:(1)∵2×5=10,
∴点Q走过的路程是1+2+3+4=10,Q处于:1﹣2+3﹣4=4﹣6=﹣2;
(2)①当点A在原点左边时,设需要第n次到达点A,则![]() =20,解得n=39,
=20,解得n=39,
∴动点Q走过的路程是
1+|﹣2|+3+|﹣4|+5+…+|﹣38|+39,
=1+2+3+…+39,
=![]() =780,
=780,
∴时间=780÷2=390秒(6.5分钟);
②当点A原点左边时,设需要第n次到达点A,则![]() =20,
=20,
解得n=40,
∴动点Q走过的路程是
1+|﹣2|+3+|﹣4|+5+…+39+|﹣40|,
=1+2+3+…+40,
=![]() =820,
=820,
∴时间=820÷2=410秒 (6![]() 分钟).
分钟).
-
科目: 来源: 题型:
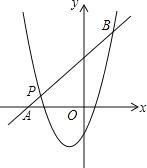
查看答案和解析>>【题目】已知二次函数y1=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.
(1)求m,n的值.
(2)如图,一次函数y2=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式.
(3)直接写出y1>y2时x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应集合的括号内
+8.5, 0, -3.4, 12, -9,
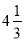 , 3.1415, -1.2,
, 3.1415, -1.2, ,
, 
(1)正数集合 { }
(2)整数集合 { }
(3)负分数集合 { }
(4)非正整数集合{ }
-
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,且E、F分别为BC、CD的中点,(如图)则∠EAF等于( )
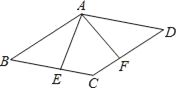
A. 75°B. 45°C. 60°D. 30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在以点O为圆心的两个同心圆中,小圆直径AE的延长线与大圆交于点B,点D在大圆上,BD与小圆相切于点F,AF的延长线与大圆相交于点C,且CE⊥BD.找出图中相等的线段并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】司机小王沿东西大街跑出租车,约定向东为正,向西为负,某天自
 地出发到收工时,行走记录为(单位:千米):+8、-9、+7、-12、+5、-10、+17、-13.
地出发到收工时,行走记录为(单位:千米):+8、-9、+7、-12、+5、-10、+17、-13.回答下列问题:
(1)收工时小王在
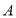 地的哪边?距
地的哪边?距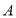 地多少千米?
地多少千米?(2)若每千米耗油0.2升,问从
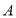 地出发到收工时,共耗油多少升?
地出发到收工时,共耗油多少升?(3)在工作过程中,小王最远离
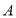 地多远?在
地多远?在 地哪边?
地哪边? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0), B(0,﹣1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.

相关试题

