【题目】司机小王沿东西大街跑出租车,约定向东为正,向西为负,某天自![]() 地出发到收工时,行走记录为(单位:千米):+8、-9、+7、-12、+5、-10、+17、-13.
地出发到收工时,行走记录为(单位:千米):+8、-9、+7、-12、+5、-10、+17、-13.
回答下列问题:
(1)收工时小王在![]() 地的哪边?距
地的哪边?距![]() 地多少千米?
地多少千米?
(2)若每千米耗油0.2升,问从![]() 地出发到收工时,共耗油多少升?
地出发到收工时,共耗油多少升?
(3)在工作过程中,小王最远离![]() 地多远?在
地多远?在![]() 地哪边?
地哪边?
参考答案:
【答案】(1)收工时小王在![]() 地的西边,距
地的西边,距![]() 地7千米;(2)从
地7千米;(2)从![]() 地出发到收工时,共耗油16.2升;(3)小王最远离
地出发到收工时,共耗油16.2升;(3)小王最远离![]() 地11千米,在
地11千米,在![]() 地的西边
地的西边
【解析】
(1)根据有理数的加法,可得答案;
(2)根据单位耗油量乘以行驶路程,可得耗油量;
(3)根据有理数的加法,可得每次与![]() 地的距离,根据有理数的大小比较,可得答案.
地的距离,根据有理数的大小比较,可得答案.
解:(1)![]() (千米),
(千米),
答:收工时小王在![]() 地的西边,距
地的西边,距![]() 地7千米;
地7千米;
(2)![]()
![]() (升),
(升),
答:从![]() 地出发到收工时,共耗油16.2升;
地出发到收工时,共耗油16.2升;
(3)第一次距![]() 地8千米,第二次距
地8千米,第二次距![]() 地
地![]() 千米,第三次距
千米,第三次距![]() 地
地![]() 千米,第四次距
千米,第四次距![]() 地
地![]() 千米,第五次距
千米,第五次距![]() 地
地![]() 千米,第六次距
千米,第六次距![]() 地
地![]() 千米,第七次距
千米,第七次距![]() 地
地![]() 千米,第八次距
千米,第八次距![]() 地
地![]() 千米,由
千米,由![]() ,
,
在工作过程中,小王最远离![]() 地11千米,在
地11千米,在![]() 地的西边.
地的西边.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,且E、F分别为BC、CD的中点,(如图)则∠EAF等于( )
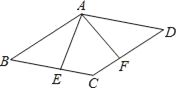
A. 75°B. 45°C. 60°D. 30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在数轴上,一动点
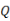 从原点
从原点 出发,沿直线以每秒钟
出发,沿直线以每秒钟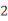 个单位长度的速度来回移动,其移动方式是先向右移动
个单位长度的速度来回移动,其移动方式是先向右移动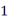 个单位长度,再向左移动
个单位长度,再向左移动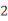 个单位长度,又向右移动
个单位长度,又向右移动 个单位长度,再向左移动
个单位长度,再向左移动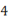 个单位长度,又向右移动
个单位长度,又向右移动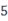 个单位长度…
个单位长度… 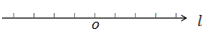
(1)求出
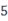 秒钟后动点
秒钟后动点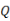 所处的位置;
所处的位置; (2)如果在数轴上还有一个定点
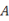 ,且
,且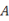 与原点
与原点 相距20个单位长度,问:动点
相距20个单位长度,问:动点 从原点出发,可能与点
从原点出发,可能与点 重合吗?若能,则第一次与点
重合吗?若能,则第一次与点 重合需多长时间?若不能,请说明理由.
重合需多长时间?若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在以点O为圆心的两个同心圆中,小圆直径AE的延长线与大圆交于点B,点D在大圆上,BD与小圆相切于点F,AF的延长线与大圆相交于点C,且CE⊥BD.找出图中相等的线段并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0), B(0,﹣1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.

-
科目: 来源: 题型:
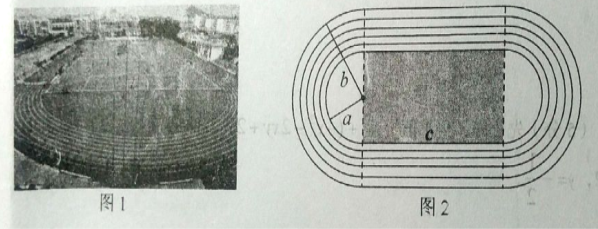
查看答案和解析>>【题目】综合与实践,
如图1是某校操场实物图,图2是操场示意图,每条跑道由两条直的跑道和两端是半圆形的跑道组成,每两条跑道之间的距离是相等的,最内侧半圆形跑道的半径是a米,最外侧半圆形跑道的半径是b米,每条直道的长度都是c米。
(1)列式表示最内侧-圈跑道的长度____.(直接写出答案, 不写过程)
(2)列式表示整个操场所占地面的面积___ . (即最外侧跑道圈住的面积,直接写出答案,不写过程)
(3)新学期,学校为了给学生们提供优美的校园环境和锻炼场所,改造并美化操场,跑道内部的长方形部分(图中阴影部分)设计成足球场,这部分地面铺设草坪,其余部分(即矩形外部与最外侧跑道之间的部分)铺设塑胶.兴趣小组测得a=35米,b=40米,c=100米, π取3.若草坪每平米60元,塑胶每平米80元,请你计算铺设草坪和塑胶总共花了多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,…,按此规律。则第(6)个图形中面积为1的正方形的个数为()

A. 20B. 25C. 35D. 27
相关试题

