Question

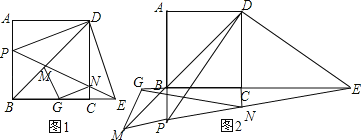
【题目】在正方形ABCD中，BD为对角线，点P从A出发，沿射线AB运动，连接PD，过点D作DE⊥PD，交直线BC于点E．

（1）当点P在线段AB上时（如图1），求证：BP+CE=BD；

（2）当点P在线段AB的延长线上时（如图2），猜想线段BP、CE、BD之间满足的关系式，并加以证明；

（3）若直线PE分别交直线BD、CD于点M、N，PM=3，EN=4，求PD的长．

Answer 1

【答案】（1）证明见解析（2）CE﹣BP=BD，理由见解析（3）3或6

【解析】

试题分析：（1）根据已知和图形证明△PAD≌△ECD，得到AP=CE，根据AB=BD，得到答案；

（2）与（1）的方法类似，求出结论；

（3）分P在线段AB上和P在AB延长线上两种情况进行讨论，根据三角形全等和勾股定理证明结论．

证明：（1）∵四边形ABCD是正方形，

∴∠A=∠ADC=∠BCD=∠DCE=90°，AD=CD，

∵DE⊥PD，

∴∠ADC=∠PDE=90°，

∴∠ADP=90°﹣∠PDC=∠CDE，

∴△PAD≌△ECD，

∴AP=CE，

∴BP+CE=BP+AP=AB=BD；

（2）CE﹣BP=BD；

理由：△PAD≌△ECD，

∴CE=AP，

∴CE﹣BP=AP﹣BP=AB=BD；

（3）①当P在线段AB上时，

如图1所示，在BC上取一点G使得BG=BP，连接MG、NG，

∵△APD≌△CED，

∵AP=CE，PD=ED，

∴△PED是等腰直角三角形，

∴AB=BC=AP+BP=BG+CG，

∴CG=CE，

∴可证△NCG≌△NCE，

∴NG=NE，∠NGC=∠NEC，

∵∠PBM=∠GBM=45°，BP=BG，BM=BM，

∴△BPM≌△BGM

∴PM=GM，∠MGB=∠MPB，

又∠NEC+∠MPB=90°，

∴∠NGC+∠MGB=90°，

∴∠MGN=90°，

∴MN==5，

∴PE=PM+MN+EN=3+5+4=12，

∴PD=PE=6；

②当P在AB延长线上时，

如图2所示，延长CB至G，使得CG=CE，连接MG、NG，

∵AP=CE，

∴CE﹣BC=CG﹣BC=AP﹣AB=BP=BG，

同①可证△△BMG≌△BMP，△CNG≌△CNE，

∴PM=GM，GN=EN，∠BGM=∠BPM=90°+∠CEN=90°+CGN，

∴∠CGN=∠BGM﹣90°=∠BGM﹣∠MGN，

∴∠MGN=90°，

∴MN==5，

∴PN=MN﹣PM=5﹣3=2，

∴PE=PN+EN=2+4=6，

∴PD=PE=3，

∴PD的长为3或6．