【题目】如图1，在直角坐标系xoy中，O是坐标原点，点A在x正半轴上，OA＝cm，点B在y轴的正半轴上，OB＝12cm，动点P从点O开始沿OA以cm/s的速度向点A移动，动点Q从点A开始沿AB以4cm/s的速度向点B移动，动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动，移动时间为t（0＜t＜6）s.

（1）求∠OAB的度数.

（2）以OB为直径的⊙O′与AB交于点M，当t为何值时，PM与⊙O′相切？

（3）是否存在△RPQ为等腰三角形？若存在，请直接写出出的t值；若不存在，请说明理由．

参考答案：

【答案】(1) 30°．(2) t=3时，PM与⊙O’相切．(3) t=8-2， ，1+时，△RPQ为等腰三角形．

【解析】试题分析：（1）在Rt△OAB中，已知了OA、OB的长，即可求出∠OAB的正切值，由此可得到∠OAB的度数；

（2）连接O′M，当PM与⊙O′相切时，PM、PO同为⊙O′的切线，易证得△OO′P≌△MO′P，则∠OO′P=∠MO′P；在（1）中易得∠OBA=60°，即△O′BM是等边三角形，由此可得到∠BO′M=∠PO′M=∠PO′O=60°；在Rt△OPO′中，根据∠PO′O的度数及OO′的长即可求得OP的长，已知了P点的运动速度，即可根据时间=路程÷速度求得t的值；

（3）存在△RPQ为等腰三角形，由于△QPQ的腰和底不确定，需分类讨论：①PR=RQ，②PR=PQ，③RQ=PQ时分别求出符合题意的t值即可，

试题解析：（1）在Rt△AOB中：

tan∠OAB=，

∴∠OAB=30°．

（2）如图，连接O′P，O′M．

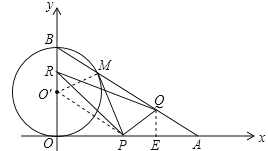
当PM与⊙O′相切时，有：

∠PMO′=∠POO′=90°，

△PMO′≌△POO′．

由（1）知∠OBA=60°，

∵O′M=O′B，

∴△O′BM是等边三角形，

∴∠BO′M=60°．

可得∠OO′P=∠MO′P=60°．

∴OP=OO′tan∠OO′P

=6×tan60°=6，

又∵OP=2t，

∴2t=6，

t=3．

即：t=3时，PM与⊙O’相切．

（3）存在△RPQ为等腰三角形，

理由如下：由题意可知：PR2=16t2-48t，PQ2=52t2-288t，RQ2=28t2-240t+576，

当①PR=RQ时，可得t=8-2（t=8+舍去）；

当②PR=PQ时，可得t=；

当③RQ=PQ时，可得t=1+（t=1-舍去）

综上可知：当t=8-2， ，1+时，△RPQ为等腰三角形．

关闭