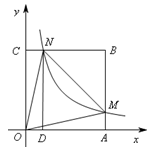
【题目】如图,在直角坐标系中,正方形OABC的顶点O与原点重合,顶点A.C分别在x轴、y轴上,反比例函数![]() 的图象与正方形的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN.下列结论:
的图象与正方形的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN.下列结论:
①△OCN≌△OAM;
②ON=MN;
③四边形DAMN与△MON面积相等;
④若∠MON=450,MN=2,则点C的坐标为![]() .
.
其中正确的个数是( )
A.1 B.2 C.3 D.4
参考答案:
【答案】C.
【解析】
试题分析:设正方形OABC的边长为a,
则A(a,0),B(a,a),C(0,a),M(a,![]() ),N(
),N(![]() ,a).
,a).
∵CN=AM=![]() ,OC=OA= a,∠OCN=∠OAM=900,∴△OCN≌△OAM(SAS).结论①正确.
,OC=OA= a,∠OCN=∠OAM=900,∴△OCN≌△OAM(SAS).结论①正确.
根据勾股定理,![]() ,
,![]() ,∴ON和MN不一定相等.结论②错误.
,∴ON和MN不一定相等.结论②错误.
∵![]() ,∴
,∴![]() .结论③正确.
.结论③正确.
如图,过点O作OH⊥MN于点H,则
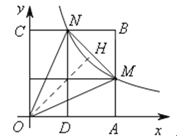
∵△OCN≌△OAM ,∴ON=OM,∠CON=∠AOM.
∵∠MON=450,MN=2,∴NH=HM=1,∠CON=∠NOH=∠HOM=∠AOM=22.50.
∴△OCN≌△OHN(ASA).∴CN=HN=1.∴![]() ,即
,即![]() .
.
由![]() ,得:
,得:![]() ,∴
,∴![]() ,∴
,∴![]() .
.
解得:![]() (舍去负值).
(舍去负值).
∴点C的坐标为![]() .结论④正确.∴结论正确的为①③④3个.故选C.
.结论④正确.∴结论正确的为①③④3个.故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个平行四边形中,若一个角的平分线把一条边分成长是2cm和3cm的两条线段,求该平行四边形的周长是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
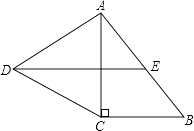
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣5a2(3ab2﹣6a3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y2(x2)21是由y2x2怎样平移得到的( )
A.先向左平移2个单位长度,再向上平移1个单位长度
B.先向左平移2个单位长度,再向下平移1个单位长度
C.先向右平移2个单位长度,再向上平移1个单位长度
D.先向右平移2个单位长度,再向下平移1个单位长度
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|x﹣1|+(y+2)2=0,则(x+y)2017= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
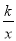 ,当x=-
,当x=-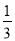 时,y=-6.
时,y=-6.(1)这个函数的图象位于哪些象限?y随x的增大如何变化?
(2)当
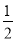 <x<4时,求y的取值范围.
<x<4时,求y的取值范围.
相关试题

