【题目】如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE. 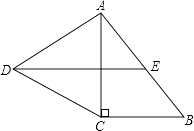
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
参考答案:
【答案】
(1)证明:连结CE.
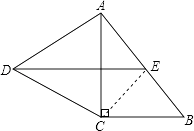
∵点E为Rt△ACB的斜边AB的中点,
∴CE= ![]() AB=AE.
AB=AE.
∵△ACD是等边三角形,
∴AD=CD.
在△ADE与△CDE中, 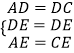 ,
,
∴△ADE≌△CDE(SSS),
∴∠ADE=∠CDE=30°.
∵∠DCB=150°,
∴∠EDC+∠DCB=180°.
∴DE∥CB
(2)解:当AC= ![]() 或AB=2AC时,四边形DCBE是平行四边形,
或AB=2AC时,四边形DCBE是平行四边形,
理由:∵AC= ![]() ,∠ACB=90°,
,∠ACB=90°,
∴∠B=30°,
∵∠DCB=150°,
∴∠DCB+∠B=180°,
∴DC∥BE,又∵DE∥BC,
∴四边形DCBE是平行四边形.
【解析】(1)首先连接CE,根据直角三角形的性质可得CE= ![]() AB=AE,再根据等边三角形的性质可得AD=CD,然后证明△ADE≌△CDE,进而得到∠ADE=∠CDE=30°,再有∠DCB=150°可证明DE∥CB;(2)当AC=
AB=AE,再根据等边三角形的性质可得AD=CD,然后证明△ADE≌△CDE,进而得到∠ADE=∠CDE=30°,再有∠DCB=150°可证明DE∥CB;(2)当AC= ![]() 或AB=2AC时,四边形DCBE是平行四边形.根据(1)中所求得出DC∥BE,进而得到四边形DCBE是平行四边形.
或AB=2AC时,四边形DCBE是平行四边形.根据(1)中所求得出DC∥BE,进而得到四边形DCBE是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式2x﹣y的值是5,则代数式4x﹣2y﹣13的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式x2﹣(k+1)x+9是完全平方式,则k=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个平行四边形中,若一个角的平分线把一条边分成长是2cm和3cm的两条线段,求该平行四边形的周长是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣5a2(3ab2﹣6a3)
-
科目: 来源: 题型:
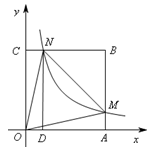
查看答案和解析>>【题目】如图,在直角坐标系中,正方形OABC的顶点O与原点重合,顶点A.C分别在x轴、y轴上,反比例函数
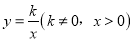 的图象与正方形的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN.下列结论:
的图象与正方形的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN.下列结论:①△OCN≌△OAM;
②ON=MN;
③四边形DAMN与△MON面积相等;
④若∠MON=450,MN=2,则点C的坐标为
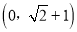 .
.其中正确的个数是( )
A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y2(x2)21是由y2x2怎样平移得到的( )
A.先向左平移2个单位长度,再向上平移1个单位长度
B.先向左平移2个单位长度,再向下平移1个单位长度
C.先向右平移2个单位长度,再向上平移1个单位长度
D.先向右平移2个单位长度,再向下平移1个单位长度
相关试题

