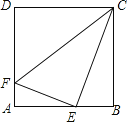
【题目】已知正方形ABCD的边长为4,E为AB的中点,F为AD上一点,且AF=![]() AD,试判断△EFC的形状.
AD,试判断△EFC的形状.
参考答案:
【答案】△EFC为直角三角形,理由见解析
【解析】
因为正方形ABCD的边长为4,易得AF=1,则FD=3,DC=BC=4,AE=EB=2;在Rt△AEF、Rt△DFC,Rt△EBC中,利用勾股定理求出EF、EC、FC的长,再根据勾股定理的逆定理解答.
解:△EFC为直角三角形.
∵正方形ABCD的边长为4,AF=![]() AD
AD
∴AF=1,FD=3,DC=BC=4,
∵E为AB的中点,
∴AE=EB=2;
在Rt△AEF中,EF=![]() ;
;
在Rt△DFC中,FC=![]() =5;
=5;
在Rt△EBC中,EC=![]() =2
=2![]() .
.
∴EC2+EF2=FC2,
∴△EFC是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列不等式(组)
(1)3x+8≤5x-12
(2)2x<1-x≤x+5,并写出它的所有整数解.
(3)

(4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知DE∥BC,∠3=∠B,则∠1+∠2=180°.下面是王宁同学的思考过程,请你在括号内填上理由、依据或内容。

思考过程
因为 DE∥BC(已知)
所以∠3=∠EHC ( )
因为∠3=∠B(已知)
所以∠B=∠EHC ( )
所以 AB∥EH ( )
∠2+ ( )=180°( )
因为∠1=∠4( )
所以∠1+∠2=180°(等量代换)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A、B 两点分别位于一个池塘的两端,小明想用绳子测量A、B 间的距离,但绳子不够长,请你利用三角形全等的相关知识帮他设计一种方案测量出A、B间的距离,写出具体的方案,并解释其中的道理,

-
科目: 来源: 题型:
查看答案和解析>>【题目】为切实做好校园疫情防控和开学的各项准备工作,某校准备再次购进免手洗消毒凝胶和医用口罩用于防疫,若购进30箱医用口罩和20箱免手洗消毒凝胶共需8500元;若购进40箱医用口罩和10箱免手洗消毒凝胶共需8000元.
(1)求医用口罩和免手洗消毒凝胶每箱购进价格分别为多少元?
(2)若该校购进免手洗消毒凝胶的数量比购进医用口罩数量的2倍少10箱,且用于购置两种物资的总经费不超过9000元,则该校至多购进医用口罩多少箱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.利用正方形网络可以画出长度为无理数的线段,如图1中
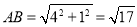 .请参考此方法按下列要求作图:
.请参考此方法按下列要求作图:(1)在图1中以格点为顶点画一个面积为17的正方形
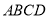 ,并标出字母;
,并标出字母;(2)在图2中以格点为顶点画一个三角形
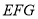 ,使
,使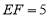 ,
,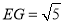 ,
,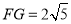 ,并标出字母;
,并标出字母;(3)猜想
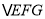 是何种特殊三角形.并说明理由.
是何种特殊三角形.并说明理由.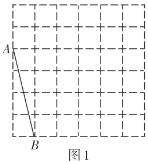

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为增加体育馆观众坐席数量,决定对体育馆进行施工改造.如图,为体育馆改造的截面示意图.已知原座位区最高点A到地面的铅直高度AC长度为15米,原坡面AB的倾斜角∠ABC为45°,原坡脚B与场馆中央的运动区边界的安全距离BD为5米.如果按照施工方提供的设计方案施工,新座位区最高点E到地面的铅直高度EG长度保持15米不变,使A、E两点间距离为2米,使改造后坡面EF的倾斜角∠EFG为37°.若学校要求新坡脚F需与场馆中央的运动区边界的安全距离FD至少保持2.5米(即FD≥2.5),请问施工方提供的设计方案是否满足安全要求呢?请说明理由.(参考数据:sin37°≈
 ,tan37°≈
,tan37°≈ )
)
相关试题

