【题目】某学校为增加体育馆观众坐席数量,决定对体育馆进行施工改造.如图,为体育馆改造的截面示意图.已知原座位区最高点A到地面的铅直高度AC长度为15米,原坡面AB的倾斜角∠ABC为45°,原坡脚B与场馆中央的运动区边界的安全距离BD为5米.如果按照施工方提供的设计方案施工,新座位区最高点E到地面的铅直高度EG长度保持15米不变,使A、E两点间距离为2米,使改造后坡面EF的倾斜角∠EFG为37°.若学校要求新坡脚F需与场馆中央的运动区边界的安全距离FD至少保持2.5米(即FD≥2.5),请问施工方提供的设计方案是否满足安全要求呢?请说明理由.(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() )
)

参考答案:
【答案】施工方提供的设计方案不满足安全要求.
【解析】试题分析:
在Rt△ABC中,由∠ACB=90°,AC=15m,∠ABC=45°可求得BC=15m;在Rt△EGD中,由∠EGD=90°,EG=15m,∠EFG=37°,可解得GF=20m;通过已知条件可证得四边形EACG是矩形,从而可得GC=AE=2m;这样可解得:DF=GC+BC+BD-GF=2+15+5-20=2<2.5,由此可知:“设计方案不满足安全要求”.
试题解析:
施工方提供的设计方案不满足安全要求,理由如下:
在Rt△ABC中,AC=15m,∠ABC=45°,
∴BC=![]() =15m.
=15m.
在Rt△EFG中,EG=15m,∠EFG=37°,
∴GF=![]() ≈
≈![]() =20m.
=20m.
∵EG=AC=15m,AC⊥BC,EG⊥BC,
∴EG∥AC,
∴四边形EGCA是矩形,
∴GC=EA=2m,
∴DF=GC+BC+BD-GF=2+15+5-20=2<2.5.
∴施工方提供的设计方案不满足安全要求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD的边长为4,E为AB的中点,F为AD上一点,且AF=
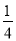 AD,试判断△EFC的形状.
AD,试判断△EFC的形状.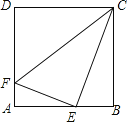
-
科目: 来源: 题型:
查看答案和解析>>【题目】为切实做好校园疫情防控和开学的各项准备工作,某校准备再次购进免手洗消毒凝胶和医用口罩用于防疫,若购进30箱医用口罩和20箱免手洗消毒凝胶共需8500元;若购进40箱医用口罩和10箱免手洗消毒凝胶共需8000元.
(1)求医用口罩和免手洗消毒凝胶每箱购进价格分别为多少元?
(2)若该校购进免手洗消毒凝胶的数量比购进医用口罩数量的2倍少10箱,且用于购置两种物资的总经费不超过9000元,则该校至多购进医用口罩多少箱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.利用正方形网络可以画出长度为无理数的线段,如图1中
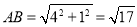 .请参考此方法按下列要求作图:
.请参考此方法按下列要求作图:(1)在图1中以格点为顶点画一个面积为17的正方形
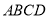 ,并标出字母;
,并标出字母;(2)在图2中以格点为顶点画一个三角形
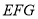 ,使
,使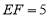 ,
,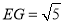 ,
,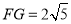 ,并标出字母;
,并标出字母;(3)猜想
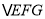 是何种特殊三角形.并说明理由.
是何种特殊三角形.并说明理由.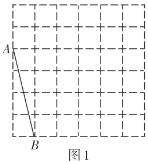

-
科目: 来源: 题型:
查看答案和解析>>【题目】暑假降至,丹尼斯大卖场为回馈新老顾客,进行有奖促销活动活动. 活动规定:购买500元的商品就可以获得一次转转盘的机会(转盘分为5个区域,分别是特等奖、一等奖、二等奖、三等奖、不获奖),转盘指针停在哪个获奖区域就可以得到该区域相应等级奖品一件(如果指针恰好停在分割线上,那么重转一次,直到指针指向某一区域为止). 大卖场工作人员在制作转盘时,将各扇形区域圆心角(不完全)分配如下表:
奖次
特等奖
一等奖
二等奖
三等奖
不获奖
圆心角


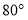

_________
促销公告:凡购买我大卖场商品500元均有可能获得下列奖品:
特等奖:山地越野自行车一辆 一等奖:双肩背包一个
二等奖:洗衣液一桶 三等奖:抽纸一盒
根据以上信息,解答下列问题:
(1)求不获奖的扇形区域圆心角度数是多少?
(2)求获得双肩背包的概率是多少?
(3)甲顾客购物520元,求他获奖的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】周六的早上,小颖去郑州图书大厦买书.她先走到早餐店吃早餐,然后又去图书大厦买书,最后又回到家.如图是小颖所用的时间 x(分)和离家的距离 y(千米)之间的示意图,请根据图像解答下列问题
(1)在上述变化过程中,自变量是 ,因变量是 ;
(2)早餐店到小颖家的距离是 千米,她早餐花了 分钟
(3)出发后37分到55分之间小颖在干什么?
(4)小颖从图书大厦回家的过程中,她的平均速度是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
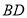 为
为 的一条对角线.
的一条对角线.(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母;(保留作图痕迹,不写作法)
①作
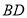 的垂直平分线
的垂直平分线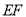 分别交
分别交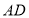 ,
,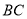 于
于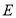 ,
,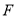 两点,交
两点,交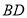 于点
于点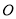 ;
;②连接
 ,
,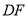 ;
;(2)猜想与证明:试猜想四边形
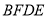 是哪种特殊的四边形,并说明理由.
是哪种特殊的四边形,并说明理由.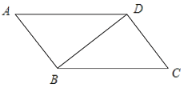
相关试题

