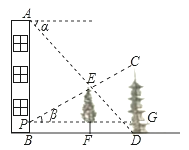
【题目】如图,在楼房AB和塔CD之间有一棵树EF,从楼顶A处经过树顶E点恰好看到塔的底部D点,且俯角α为45°.从距离楼底B点1米的P点处经过树顶E点恰好看到塔的顶部C点,且仰角β为30°.已知树高EF=6米,求塔CD的高度.(结果保留根号)
参考答案:
【答案】(1)△ACC1是等腰直角三角形(2)C2 (1,-4)(3)先将△AB1C1向右平移4个单位,然后再向下平移4个单位
【解析】试题分析:根据题意求出∠BAD=∠ADB=45°,进而根据等腰直角三角形的性质求得FD,在Rt△PEH中,利用特殊角的三角函数值分别求出BF,即可求得PG,在Rt△PCG中,继而可求出CG的长度.
试题解析:如图,

由题意可知∠BAD=∠ADB=45°,
∴FD=EF=6米,
在Rt△PEH中,∵tanβ=![]() ,
,
∴BF=![]() ,
,
∴PG=BD=BF+FD=5![]() +6,
+6,
在Rt△PCG中,∵tanβ=![]() ,
,
∴CG=(5![]() +6)
+6)![]() =5+2
=5+2![]() ,
,
∴CD=(6+2![]() )米.
)米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请你根据萌萌所给的如图所的内容,完成下列各小题.

(1)若m※n=1,m※2n=﹣2,分别求m和n的值;
(2)若m满足m※2≤0,且3m※(﹣8)>0,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 的顶点坐标为E(1,0),与
的顶点坐标为E(1,0),与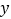 轴的交点坐标为(0,1).
轴的交点坐标为(0,1).

(1)求该抛物线的函数关系式.
(2)A、B是
 轴上两个动点,且A、B间的距离为AB=4,A在B的左边,过A作AD⊥
轴上两个动点,且A、B间的距离为AB=4,A在B的左边,过A作AD⊥ 轴交抛物线于D,
轴交抛物线于D,过B作BC⊥
 轴交抛物线于C. 设A点的坐标为(
轴交抛物线于C. 设A点的坐标为(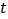 ,0),四边形ABCD的面积为S.
,0),四边形ABCD的面积为S.① 求S与
 之间的函数关系式.
之间的函数关系式.② 求四边形ABCD的最小面积,此时四边形ABCD是什么四边形?
③ 当四边形ABCD面积最小时,在对角线BD上是否存在这样的点P,使得△PAE的周长最小,若存在,请求出点P的坐标及这时△PAE的周长;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:(1)
 ;(2)
;(2) ;
; (3)
 ;(4)
;(4)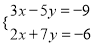
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校共有5个大餐厅和2个小餐厅.经过测试:同时开放1个大餐厅、2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅、1个小餐厅,可供2280名学生就餐.求1个大餐厅、1个小餐厅分别可供多少名学生就餐.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,以点(3,2)为圆心、2为半径的圆,一定( )
A. 与x轴相切,与y轴相切B. 与x轴相切,与y轴相离
C. 与x轴相离,与y轴相切D. 与x轴相离,与y轴相离
-
科目: 来源: 题型:
查看答案和解析>>【题目】森林公园的门票价格规定如下表:
购票人数
1~50人
51~100人
100人以上
每人门票价
13元
11元
9元
某校初一(5)(6)两个班共104人去游森林公园,其中(5)班人数较少,不到50人;(6)班人数较多,(6)班人数多于50人且少于100人.经估算,如果两班都是以班为单位分别购票则一共应付1240元;
(1)求这两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少元?
相关试题

