【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,且
点,且![]() .
.

![]() 求抛物线的解析式及顶点
求抛物线的解析式及顶点![]() 的坐标;
的坐标;
![]() 判断
判断![]() 的形状,证明你的结论;
的形状,证明你的结论;
![]() 点
点![]() 是
是![]() 轴上的一个动点,当
轴上的一个动点,当![]() 的周长最小时,求点
的周长最小时,求点![]() 的坐标.
的坐标.
参考答案:
【答案】![]()
![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ;
;![]() 是直角三角形.理由见解析;
是直角三角形.理由见解析;![]()
![]() .
.
【解析】
(1)、将点A的坐标代入解析式得出b的值,从而得出函数解析式,将解析式进行配方得出顶点坐标;(2)、根据函数解析式得出点B和点C的坐标,从而得出AB、AC和BC的长度,从而得出三角形的形状;(3)、作出点C关于x轴的对应点![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,利用待定系数法求出直线
,利用待定系数法求出直线![]() 的解析式,从而得出点M的坐标.
的解析式,从而得出点M的坐标.
![]() ∵点
∵点![]() 在抛物线
在抛物线![]() 上,∴
上,∴![]() ,
,
解得![]() ,∴抛物线的解析式为
,∴抛物线的解析式为![]() .
.
∵![]() ,∴顶点
,∴顶点![]() 的坐标为
的坐标为![]() ;
;
![]() 是直角三角形.理由如下:当
是直角三角形.理由如下:当![]() 时,
时,![]() ,∴
,∴![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,∴
,∴![]() ,
,![]() ,则
,则![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() . ∵
. ∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() 是直角三角形;
是直角三角形;
![]() 作出点
作出点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,则
,则![]() .
.
连接![]() 交
交![]() 轴于点
轴于点![]() ,
,
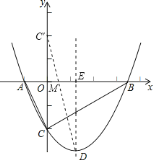
根据轴对称性及两点之间线段最短可知,![]() 一定,当
一定,当![]() 的值最小时,
的值最小时,![]() 的周长最小.
的周长最小.
设直线![]() 的解析式为
的解析式为![]() ,则
,则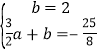 ,解得
,解得![]() ,
,
∴![]() .
.
当![]() 时,
时,![]() ,则
,则![]() , ∴
, ∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在某场足球比赛中,球员甲从球门底部中心点
 的正前方
的正前方 处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为
处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为 时达到最高点,此时足球飞行的水平距离为
时达到最高点,此时足球飞行的水平距离为 .已知球门的横梁高
.已知球门的横梁高 为
为 .
.
 在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况) 守门员乙站在距离球门
守门员乙站在距离球门 处,他跳起时手的最大摸高为
处,他跳起时手的最大摸高为 ,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门? -
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小亮进行百米赛跑,小明比小亮跑得快,如果两人同时起跑,小明肯定赢,现在小明让小亮先跑若干米,图中
 ,
, 分别表示两人的路程与小明追赶时间的关系.
分别表示两人的路程与小明追赶时间的关系.
(1)哪条线表示小明的路程与时间之间的关系?
(2)小明让小亮先跑了多少米?
(3)谁将赢得这场比赛?
(4)
 对应的一次函数表达式中,一次项系数是多少?它的实际意义是什么?
对应的一次函数表达式中,一次项系数是多少?它的实际意义是什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).

(1)在图中作出
 关于
关于 轴对称的
轴对称的 .
.(2)写出点
 的坐标(直接写答案).
的坐标(直接写答案).A1_____________,B1______________,C1______________
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图①,在△ABC中,BC=AC,在△CDE中,CE=CD,现把两个三角形的C点重合,且使∠BCA=∠ECD,连接BE、AD.
(1)求证:BE=AD
(2)若将△ECD绕点C旋转至图②、③所示的情况时,其余条件不变,BE与AD还相等么?若相等,请给与证明;若不相等,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,抛物线
中,抛物线 与
与 轴的交点分别为
轴的交点分别为 ,
, .
. 求证:抛物线总与
求证:抛物线总与 轴有两个不同的交点;
轴有两个不同的交点; 若
若 ,求此抛物线的解析式.
,求此抛物线的解析式. 已知
已知 轴上两点
轴上两点 ,
, ,若抛物线
,若抛物线 与线段
与线段 有交点,请写出
有交点,请写出 的取值范围.
的取值范围.
相关试题

