【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() .
.
![]() 求证:抛物线总与
求证:抛物线总与![]() 轴有两个不同的交点;
轴有两个不同的交点;
![]() 若
若![]() ,求此抛物线的解析式.
,求此抛物线的解析式.
![]() 已知
已知![]() 轴上两点
轴上两点![]() ,
,![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() 有交点,请写出
有交点,请写出![]() 的取值范围.
的取值范围.
参考答案:
【答案】![]() 证明见解析;
证明见解析;![]()
![]() ;
;![]()
![]() .
.
【解析】
(1)、证明△>0即可;(2)、利用抛物线与x轴的交点问题,则![]() 、
、![]() 为方程m
为方程m![]() -8mx+16m-1=0的两根,利用根与系数的关系得到
-8mx+16m-1=0的两根,利用根与系数的关系得到![]() +
+![]() =8,
=8,![]() =
=![]() ,再变形|
,再变形|![]() |=2得到
|=2得到![]() ,然后解出m即可得到抛物线解析式;(3)、先求出抛物线的对称轴为直线x=4,利用函数图象,由于抛物线开口向上,则只要当x=2,y≥0时,抛物线与线段CD有交点,于是得到4m-16m+16m-1≥0,然后解不等式即可.
,然后解出m即可得到抛物线解析式;(3)、先求出抛物线的对称轴为直线x=4,利用函数图象,由于抛物线开口向上,则只要当x=2,y≥0时,抛物线与线段CD有交点,于是得到4m-16m+16m-1≥0,然后解不等式即可.
![]() 、证明:
、证明:![]() , ∵
, ∵![]() ,∴
,∴![]() ,
,
∴抛物线总与![]() 轴有两个不同的交点;
轴有两个不同的交点;
![]() 、根据题意,
、根据题意,![]() 、
、![]() 为方程
为方程![]() 的两根,
的两根,
∴![]() ,
,![]() , ∵
, ∵![]() ,
,
∴![]() , ∴
, ∴![]() , ∴
, ∴![]() ,
,
∴抛物线的解析式为![]() ;
;
![]() 、抛物线的对称轴为直线
、抛物线的对称轴为直线![]() ,
,
∵抛物线开口向上, ∴当![]() ,
,![]() 时,抛物线与线段
时,抛物线与线段![]() 有交点,
有交点,
∴![]() , ∴
, ∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与 轴交于
轴交于 、
、 两点,与
两点,与 轴交于
轴交于 点,且
点,且 .
.
 求抛物线的解析式及顶点
求抛物线的解析式及顶点 的坐标;
的坐标; 判断
判断 的形状,证明你的结论;
的形状,证明你的结论; 点
点 是
是 轴上的一个动点,当
轴上的一个动点,当 的周长最小时,求点
的周长最小时,求点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图①,在△ABC中,BC=AC,在△CDE中,CE=CD,现把两个三角形的C点重合,且使∠BCA=∠ECD,连接BE、AD.
(1)求证:BE=AD
(2)若将△ECD绕点C旋转至图②、③所示的情况时,其余条件不变,BE与AD还相等么?若相等,请给与证明;若不相等,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,O为坐标原点,A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( )
A.4个B.3个C.2个D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】悦达汽车4S店“十一”黄金周销售某种型号汽车,该型号汽车的进价为30万元/辆,若黄金周期间销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,黄金周期间销售量不会突破30台.已知该型号汽车的销售价为32万元/辆,悦达汽车4S店计划黄金周期间销售利润25万元,那么需售出多少辆汽车?(注:销售利润=销售价﹣进价)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某幼儿园有一道长为
 米的墙,计划用
米的墙,计划用 米长的围栏利用一面墙如图围成一个矩形草坪
米长的围栏利用一面墙如图围成一个矩形草坪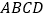 .设该矩形草坪
.设该矩形草坪 边的长为
边的长为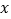 米,面积为
米,面积为 平方米.
平方米. 求出
求出 与
与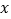 的函数关系式并写出
的函数关系式并写出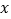 的取值范围;
的取值范围;
 如果所围成的矩形草坪面积为
如果所围成的矩形草坪面积为 平方米,试求
平方米,试求 边的长;
边的长; 按题目的设计要求,________(填“能”或“不能”)围成面积为
按题目的设计要求,________(填“能”或“不能”)围成面积为 平方米的矩形草坪.
平方米的矩形草坪.
相关试题

