【题目】在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A第,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
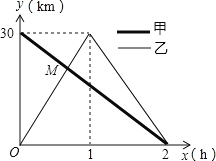
(1)A、B两地之间的距离: km;
(2)甲的速度为 km/h;乙的速度为30km/h;
(3)点M的坐标为 ;
(4)求:甲离B地的距离y(km)与行驶时间x(h)之间的函数关系式(不必写出自变量的取值范围).
参考答案:
【答案】(1)30;(2)15;(3)(![]() ,20);(4)y=-15x+30.
,20);(4)y=-15x+30.
【解析】
试题分析:(1)根据函数图象就可以得出A、B两地的距离;
(2)根据函数图象反应的时间即可求出甲乙的速度;
(3)根据函数图象反应的时间可以求出甲乙的速度,就可以求出相遇时间,就可以求出乙离B地的距离而得出相遇点M的坐标;
(4)设甲离B地的距离y(km)与行驶时间x(h)的函数关系式为y=kx+b,把(0,20),(2,0)代入即可解答.
试题分析:(1)由函数图象,得
A、B两地的距离为30千米.
答:A、B两地的距离为30千米;
(2)由函数图象,得
甲的速度为:30÷2=15千米/时,
乙的速度为:30÷1=30千米/时;
(3)甲乙相遇的时间为:30÷(15+30)=![]() 小时.
小时.
相遇时乙离开B地的距离为:![]() ×30=20千米.
×30=20千米.
∴M(![]() ,20),
,20),
表示![]() 小时时两车相遇,此时距离B地20千米;
小时时两车相遇,此时距离B地20千米;
(4)设:y=kx+b,
根据题意得![]()
解得k=-15,
所以所求函数关系式为y=-15x+30.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD中,AD=BC=6,AB=CD=4.点P从点A出发,以每秒1个单位的速度沿A→B→C→D→A的方向运动,回到点A停止运动.设运动时间为t秒.
(1)当t= 时,点P到达点C;当t= 时,点P回到点A;
(2)△ABP面积取最大值时t的取值范围;(3)当△ABP的面积为3时,求t的值;
(4)若点P出发时,点Q从点A出发,以每秒2个单位的速度沿A→D→C→B→A的方向运动,回到点A停止运动.请问:P 、Q何时在长方形ABCD的边上相距1个单位长度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是一个正方体的表面展开图,请回答下列问题:
(1)与面B,C相对的面分别是 ;
(2)若A=a3+
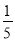 a2b+3,B=﹣
a2b+3,B=﹣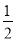 a2b+a3,C=a3﹣1,D=﹣
a2b+a3,C=a3﹣1,D=﹣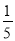 (a2b+15),且相对两个面所表示的代数式的和都相等,求E,F分别代表的代数式.
(a2b+15),且相对两个面所表示的代数式的和都相等,求E,F分别代表的代数式.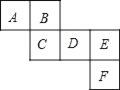
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A(-2,0) ,B(-1,2) ,C(1,0) ,连接 AB,点 D 为 AB 的中点,连接 OB 交 CD于点 E,则四边形 DAOE 的面积为( )
A. 1. B.
 C.
C. 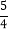 D.
D. 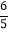
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则A2017的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD∥EF,∠1=75,∠2=45,点 G为∠BED 内一点,且 EG把∠BED分成 1 ∶ 2 两部分,则∠GEF 的度数为 ___.
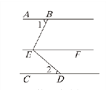
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,过对角线BD上任意一点P,作EF∥BC,GH∥AB,下列结论:①图中共有3个菱形;②△BEP≌△BGP;③四边形AEPH的面积等于△ABD的面积的一半;④四边形AEPH的周长等于四边形GPFC的周长.其中正确的是________.(填序号)

相关试题

