【题目】将△ABC的∠C折起,翻折后角的顶点位置记作C′,当C′落在AC上时(如图1),易证:∠1=2∠2.
当C′点落在CA和CB之间(如图2)时,或当C′落在CB、CA的同旁(如图3)时,∠1、∠2、∠3关系又如何?请写出你的猜想,并就其中一种情况给出证明.
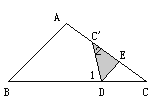
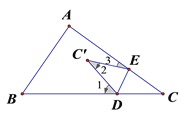
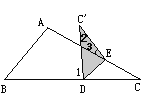
图1 图2 图3
参考答案:
【答案】见解析
【解析】利用轴对称的知识找出等解即可进行推理判断.
解:当C′点落在CA和CB之间(如图2)时,∠1+∠3=2∠2;
当C′落在CB、CA的同旁(如图3)时,∠1-∠3=2∠2;
对于图2证明如下:
连结CC’,如图4所示,
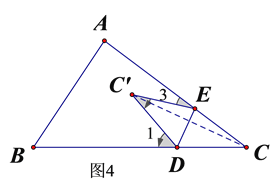
∵⊿EC’D是由⊿ECD翻折得到的,
∴⊿EC’D≌⊿ECD,由此得EC=EC’,DC=DC’,∠EC’D=∠ECD,
∴∠EC’C=∠ECC;∠DC’C=∠DCC,
∵∠1=∠DC’C+∠DCC’ ,∠3=∠EC’C+∠ECC’ ,
∴∠1+∠3=∠DC’C+∠DCC’ +∠ EC’C+∠ECC’=2∠DC’C+2∠ EC’C =2(∠DC’C+∠ EC’C)= 2∠2;
∴∠1+∠3=2∠2;
对于图3证明如下:
设AC与DC’在⊿ABC内部所夹角为∠4,如图5所示,
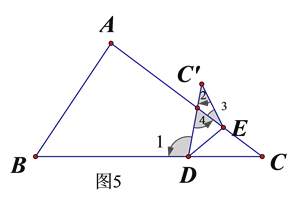
则有∠1=∠C+∠4,∠4=∠3+∠2,
又由翻折得:∠2=∠C,
∴∠1=∠2+∠3+∠2=∠3+2∠2,
∴∠1-∠3=2∠2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=ax+b(a≠0)的图象与反比例函数y=
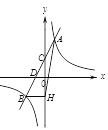
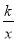 (k≠0)的图象相交于A、B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-1,0),点A的横坐标是1,tan∠CDO=2,过点B作BH⊥y轴于点H,连接 AH.
(k≠0)的图象相交于A、B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-1,0),点A的横坐标是1,tan∠CDO=2,过点B作BH⊥y轴于点H,连接 AH.(1)求一次函数和反比例函数的解析式;(2)求△ABH的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=
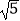 ,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F. 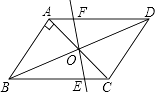
(1)证明:当∠AOF=90°时,四边形ABEF是平行四边形;
(2)试说明在旋转过程中,AF与CE总保持相等;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时∠AOF度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,线段A'B'是由线段AB经过平移得到的,已知点A(2,1)的对应点为A'(3,1),点B的对应点为B'(4,0),则点B的坐标为( )
A.(9,2)B.(1,2)C.(1,3)D.(1,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个数能否被99整除是从这个数的末位开始,两位一段,看看这些数段的和能否被99整除。像这样能够被99整除的数,我们称之为“长久数”。例如542718,因为18+27+54=99,所以542718能够被99整除;又例如25146,因为46+51+2=99,所以25146能够被99整除。
(1)若
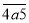 这个三位数是“长久数”,求a的值;
这个三位数是“长久数”,求a的值;(2)在(1)中的三位数的首位和个位与十位之间加上和为9的两个数字,让其成为一个五位数,该五位数仍是“长久数”,求这个五位数;
-
科目: 来源: 题型:
查看答案和解析>>【题目】掷一枚正方体的骰子,各个面上分别标有数字1, 2,3,4,5,6,求下列事件发生的频率的大小:
①朝上的数字是奇数;
②朝上的数字能被3除余1;
③朝上的数字不是3的倍数;
④朝上的数字小于6;
⑤朝上的数字不小于3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点(1,m),(2,n)都在函数y=﹣2x+1的图象上,则m、n的大小关系是( )
A. m=n B. m<n C. m>n D. 不确定
相关试题

