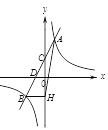
【题目】一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象相交于A、B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-1,0),点A的横坐标是1,tan∠CDO=2,过点B作BH⊥y轴于点H,连接 AH.
(k≠0)的图象相交于A、B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-1,0),点A的横坐标是1,tan∠CDO=2,过点B作BH⊥y轴于点H,连接 AH.
(1)求一次函数和反比例函数的解析式;(2)求△ABH的面积.
参考答案:
【答案】(1)一次函数解析式为: ![]() ;反比例函数的解析式为:
;反比例函数的解析式为: ![]() ;
;
(2)![]()
【解析】分析:(1)由题意利用已知条件可求出A的坐标,再利用待定系数法确定反比例函数y=![]() 中的k值,然后根据一次函数y=ax+b过A(2,2),D(-2,0),也利用待定系数法确定函数解析式;
中的k值,然后根据一次函数y=ax+b过A(2,2),D(-2,0),也利用待定系数法确定函数解析式;
(2)由反比例函数和直线有交点得到![]() ,解方程即可求出B的坐标,然后利用割补法就可以得到S△AOB=S△AOD+S△BOD,利用已知条件即可解决问题.
,解方程即可求出B的坐标,然后利用割补法就可以得到S△AOB=S△AOD+S△BOD,利用已知条件即可解决问题.
本题解析:
(1)解: ![]() D(-1,0)
D(-1,0) ![]() OD=1 又
OD=1 又![]()
![]()
![]() C(0,2)
C(0,2)
![]() D(-1,0)和C(0,2)在y=ax+b上
D(-1,0)和C(0,2)在y=ax+b上 ![]()
![]() 解得:
解得: ![]()
![]()
![]()
![]() A 在y=2x+2上且
A 在y=2x+2上且![]() =1
=1 ![]()
![]()
![]() A(1,4)
A(1,4) ![]() A在
A在![]() 上
上 ![]() k=xy=4
k=xy=4 ![]() 反比例:
反比例: ![]()
(2)联立y=2x+2和![]() 得:
得: ![]() ,解得:x=-2或x=1
,解得:x=-2或x=1![]() B(-2,2) ,
B(-2,2) ,
![]() BH垂直于y轴,且H在y轴上
BH垂直于y轴,且H在y轴上 ![]() H(0,-2)
H(0,-2) ![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店今年1月份购进一批笔记本,共2290本,每本进价为10元,该文具店决定从2月份开始进行销售,若每本售价为11元,则可全部售出;且每本售价每增加0.5元,销量就减少15本.
(1)若该种笔记本在2月份的销售量不低于2200本,则2月份售价应不高于多少元?
(2)由于生产商提高工艺,该笔记本的进价提高了10%,文具店为了增加笔记本的销量, 进行了销售调整,售价比2月份在(1)的条件下的最高售价减少了
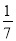 m%,结果3月份的销量比2月份在(1)的条件下的最低销量增加了m%,3月份的销售利润达到 6600元,求m的值.
m%,结果3月份的销量比2月份在(1)的条件下的最低销量增加了m%,3月份的销售利润达到 6600元,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列单项式:x,﹣3x2 , 5x3 , ﹣7x4 , 9x5 , …按此规律,可以得到第2016个单项式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记数法表示这个数235 000 000为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=
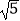 ,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F. 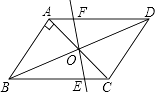
(1)证明:当∠AOF=90°时,四边形ABEF是平行四边形;
(2)试说明在旋转过程中,AF与CE总保持相等;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时∠AOF度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,线段A'B'是由线段AB经过平移得到的,已知点A(2,1)的对应点为A'(3,1),点B的对应点为B'(4,0),则点B的坐标为( )
A.(9,2)B.(1,2)C.(1,3)D.(1,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将△ABC的∠C折起,翻折后角的顶点位置记作C′,当C′落在AC上时(如图1),易证:∠1=2∠2.
当C′点落在CA和CB之间(如图2)时,或当C′落在CB、CA的同旁(如图3)时,∠1、∠2、∠3关系又如何?请写出你的猜想,并就其中一种情况给出证明.
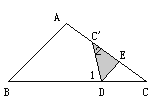
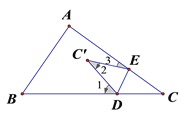
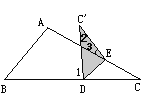
图1 图2 图3
相关试题

