【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在射线
分别在射线![]() 、
、![]() 上(点
上(点![]() 不与点
不与点![]() 、点
、点![]() 重合),且保持
重合),且保持![]() .
.
①若点![]() 在线段
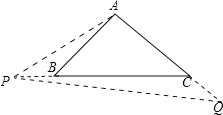
在线段![]() 上(如图),且
上(如图),且![]() ,求线段
,求线段![]() 的长;
的长;
②若![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;

参考答案:
【答案】(1)、CQ=2.4;(2)、![]() ,(0<x<8);
,(0<x<8);![]() (x≥8)
(x≥8)
【解析】
试题分析:(1)、根据∠APQ+∠CPQ=∠B+∠BAP,∠APQ=∠ABC得出∠BAP=∠CQP,然后得到△CPQ∽△BAP,根据相似比得出CQ的长度;(2)、若点P在线段CB上,根据第一题的相似比得出函数解析式;若点P在线段CB的延长线上,根据同样的方法证明△QCP∽△PBA,然后根据相似比得出函数解析式.
试题解析:(1)、∵∠APQ+∠CPQ=∠B+∠BAP,∠APQ=∠ABC,∴∠BAP=∠CQP.又∵AB=AC,∴∠B=∠C.
∴△CPQ∽△BAP.∴![]() .∵AB=AC=5,BC=8,BP=6,CP=8﹣6=2,∴
.∵AB=AC=5,BC=8,BP=6,CP=8﹣6=2,∴![]() ,
,![]() .
.
(2)、若点P在线段CB上,由(1)知![]() ,∵BP=x,BC=8,∴CP=BC﹣BP=8﹣x,
,∵BP=x,BC=8,∴CP=BC﹣BP=8﹣x,
又∵CQ=y,AB=5,∴![]() ,即
,即![]() .故所求的函数关系式为
.故所求的函数关系式为![]() ,(0<x<8).
,(0<x<8).
若点P在线段CB的延长线上,如图.∵∠APQ=∠APB+∠CPQ,∠ABC=∠APB+∠PAB,∠APQ=∠ABC,
∴∠CPQ=∠PAB.又∵∠ABP=180°﹣∠ABC,∠PCQ=180°﹣∠ACB,∠ABC=∠ACB,
∴∠ABP=∠PCQ.∴△QCP∽△PBA.∴![]() .∵BP=x,CP=BC+BP=8+x,AB=5,CQ=y,
.∵BP=x,CP=BC+BP=8+x,AB=5,CQ=y,
∴![]() ,即
,即![]() (x≥8)
(x≥8)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,CO⊥AB于点O,D在⊙O上,连接BD、CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE.
(1)求证:FD是⊙O的切线;
(2)若AF=10,tan∠BDF=
 ,求EF的长.
,求EF的长.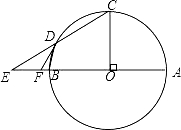
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了降低塑料袋﹣﹣“白色污染”对环境污染.学校组织了对使用购物袋的情况的调查,小明同学5月8日到站前市场对部分购物者进行了调查,据了解该市场按塑料购物袋的承重能力分别提供了0.1元,0.2元,0.3元三种质量不同的塑料袋,下面两幅图是这次调查得到的不完整的统计图(若每人每次只使用一个购物袋),请你根据图中的信息,回答下列问题:
(1)这次调查的购物者总人数是 人;
(2)请补全条形统计图,并说明扇形统计图中0.2元部分所对应的圆心角是 度,0.3元部分所对应的圆心角是 度;
(3)若5月8日到该市场购物的人数有3000人次,则该市场应销售塑料购物袋多少个?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=90°,AC=AB,点D为直线BC上的一动点,以AD为边作△ADE(顶点A、D、E按逆时针方向排列),且∠DAE=90°,AD=AE,连接CE.
⑴ 如图1,若点D在BC边上(点D与B、C不重合),求∠BCE的度数.
⑵ 如图2,若点D在CB的延长线上,若DB=5,BC=7,求△ADE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】这组数据20,21,22,23,23的中位数和众数分别是( )
A. 20,23B. 21,23C. 21,22D. 22,23
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据刘慈欣同名小说改编的电影《流浪地球》将中国独特的思想和价值观念融入对人类未来的畅想与探讨,该电影取得了巨大的成功,国内票房总收入为4 655 000 000元,用科学记数法表示4 655 000 000是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知(x2+y2+1)(x2+y2+2)=6,则x2+y2的值为。
相关试题

