【题目】为了降低塑料袋﹣﹣“白色污染”对环境污染.学校组织了对使用购物袋的情况的调查,小明同学5月8日到站前市场对部分购物者进行了调查,据了解该市场按塑料购物袋的承重能力分别提供了0.1元,0.2元,0.3元三种质量不同的塑料袋,下面两幅图是这次调查得到的不完整的统计图(若每人每次只使用一个购物袋),请你根据图中的信息,回答下列问题:
(1)这次调查的购物者总人数是 人;
(2)请补全条形统计图,并说明扇形统计图中0.2元部分所对应的圆心角是 度,0.3元部分所对应的圆心角是 度;
(3)若5月8日到该市场购物的人数有3000人次,则该市场应销售塑料购物袋多少个?

参考答案:
【答案】(1)、120; (2)、99 , 36 (3)、1875
【解析】
试题分析:(1)、根据扇形图中,每部分占总体的百分比等于该部分所对应的扇形圆心角的度数与360°的比.已知自备的有45人,占比例为![]() ;可求得总人数.(2)、根据各类别人数等于总数可得0.1元的人数,补全条形图;用各类别人数占被调查人数的比例可求得扇形统计图中0.2、0.3元元部分所对应的圆心角.(3)、用样本估计总体,按比例可估算出市场需销售塑料购物袋数目.
;可求得总人数.(2)、根据各类别人数等于总数可得0.1元的人数,补全条形图;用各类别人数占被调查人数的比例可求得扇形统计图中0.2、0.3元元部分所对应的圆心角.(3)、用样本估计总体,按比例可估算出市场需销售塑料购物袋数目.
试题解析:(1)、自备的有45人,占比例为![]() 总人数为45÷
总人数为45÷![]() =120人;
=120人;
(2)、0.1元的人数为:120﹣45﹣33﹣12=30(人),条形统计图如图所示,
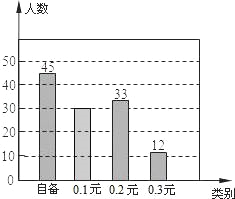
0.2元的有33人,占![]() ,其圆心角是
,其圆心角是![]() ×360°=99°
×360°=99°
0.3元的有12人,占![]() =
=![]() ,其圆心角是
,其圆心角是![]() ×360°=36°;
×360°=36°;
(3)、3000×![]() =1875
=1875
-
科目: 来源: 题型:
查看答案和解析>>【题目】一方有难八方支援,某市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型
甲
乙
丙
汽车运载量(吨/辆)
5
8
10
汽车运费(元/辆)
400
500
600
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,该市政府可以调用甲、乙、丙三种车型参与运送,已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
(3)求出那种方案的运费最省?最省是多少元. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划用104 000元购置一批电脑(这批款项须恰好用完,不得剩余或追加).经过招标,其中平板电脑每台1600元,台式电脑每台4000元,笔记本电脑每台4600元.
(1)若学校同时购进其中两种不同类型的电脑共50台,请你帮学校设计该如何购买;
(2)若学校同时购进三种不同类型的电脑共26台(三种类型的电脑都有),并且要求笔记本电脑的购买量不少于15台,请你帮学校设计购买方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,CO⊥AB于点O,D在⊙O上,连接BD、CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE.
(1)求证:FD是⊙O的切线;
(2)若AF=10,tan∠BDF=
 ,求EF的长.
,求EF的长.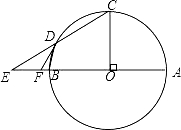
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=90°,AC=AB,点D为直线BC上的一动点,以AD为边作△ADE(顶点A、D、E按逆时针方向排列),且∠DAE=90°,AD=AE,连接CE.
⑴ 如图1,若点D在BC边上(点D与B、C不重合),求∠BCE的度数.
⑵ 如图2,若点D在CB的延长线上,若DB=5,BC=7,求△ADE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,
, ,点
,点 、
、 分别在射线
分别在射线 、
、 上(点
上(点 不与点
不与点 、点
、点 重合),且保持
重合),且保持 .
.①若点
 在线段
在线段 上(如图),且
上(如图),且 ,求线段
,求线段 的长;
的长;②若
 ,
,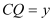 ,求
,求 与
与 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;
-
科目: 来源: 题型:
查看答案和解析>>【题目】这组数据20,21,22,23,23的中位数和众数分别是( )
A. 20,23B. 21,23C. 21,22D. 22,23
相关试题

