【题目】小刚家装修,准备安装照明灯.他和爸爸到市场进行调查,了解到某种优质品牌的一盏40瓦白炽灯的售价为1.5元,一盏8瓦节能灯的售价为22.38元,这两种功率的灯发光效果相当.假定电价为0.45元/度,设照明时间为x(小时),使用一盏白炽灯和一盏节能灯的费用分别为y1(元)和y2(元)[耗电量(度)=功率(千瓦)×用电时间(小时),费用=电费+灯的售价].
(1)分别求出y1、y2与照明时间x之间的函数表达式;
(2)你认为选择哪种照明灯合算?
(3)若一盏白炽灯的使用寿命为2000小时,一盏节能灯的使用寿命为6000小时,如果不考虑其他因素,以6000小时计算,使用哪种照明灯省钱?省多少钱?
参考答案:
【答案】
(1)解:根据题意,得y1=0.45× ![]() x+1.5,即:y1=0.018x+1.5,
x+1.5,即:y1=0.018x+1.5,
y2=0.45× ![]() x+22.38,即y2=0.0036x+22.38
x+22.38,即y2=0.0036x+22.38
(2)解:由y1=y2,得0.018x+1.5=0.0036x+22.38,解得x=1450;
由y1>y2,得0.018x+1.5>0.0036x+22.38,解得x>1450;
由y1<y2,得0.018x+1.5<0.0036x+22.38,解得x<1450.
∴当照明时间为1450小时时,选择两种灯的费用相同;当照明时间超过1450小时时,选择节能灯合算;当照明时间少于1450小时时,选择白炽灯合算
(3)解:由(2)知当x>1450小时时,使用节能灯省钱.
当x=2000时,y1=0.018×2000+1.5=37.5元;
当x=6000时,y2=0.0036×6000+22.38=43.98元,
∴3×37.5﹣43.98=68.52元.
∴按6000小时计算,使用节能灯省钱,省68.52元
【解析】(1)关键描述语:耗电量(度)=功率(千瓦)×用电时间(小时),费用=电费+灯的售价,根据已知条件,可分别列出一盏白炽灯和节能灯的费用;(2)将白炽灯与节能灯的费用列出不等式进行比较,可根据照明时间选出使用何种灯比较合算;(3)将3盏白炽灯所花费的费用和1盏节能灯所花费的费用进行比较,可知以6000小时计算,何种灯比较省钱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知xa=4,xb=3,求x3a+b的值是_______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据75, 80,85,90,80则它的众数和中位数分别为( )
A.75,80B.80,85C.80,90D.80,80
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知雅美服装厂现有A种布料70米,B种布料52米,现计划用这两种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用A种布料1.1米,B种布料0.4米,可获利50元;做一套N型号的时装需用A种布料0.6米,B种布料0.9米,可获利45元.设生产M型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.
(1)求y(元)与x(套)的函数关系式,并求出自变量的取值范围;
(2)当M型号的时装为多少套时,能使该厂所获利润最大?最大利润是多? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD内有一点P,PA=3,PB=2,PC=1,求∠BPC的度数.
分析:根据已知条件比较分散的特点,我们可以通过旋转变换将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连结PP′,这时再分别求出∠BP′P和∠AP′P的度数.
解答:(1)请你根据以上分析再通过计算求出图2中∠BPC的度数;
(2)如图3,若在正六边形ABCDEF内有一点P,且PA=2
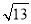 ,PB=4,PC=2,求∠BPC的度数.
,PB=4,PC=2,求∠BPC的度数.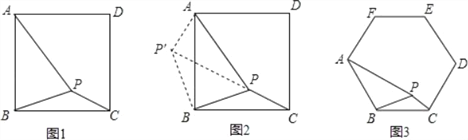
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:
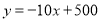 .
.(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,AB=6cm,AD=10cm,点E、F在矩形ABCD的边AB、AD上运动,将△AEF沿EF折叠,使点A′在BC边上,当折痕EF移动时,点A′在BC边上也随之移动.则A′C的取值范围为 .

相关试题

