【题目】如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的动点,P是线段BD上的一个动点,则PM+PN的最小值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】D
【解析】
作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP=NQ最小,NQ为所求,当NQ⊥AB时,NQ最小,继而利用面积法求出NQ长即可得答案.
作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP=NQ最小,NQ为所求,当NQ⊥AB时,NQ最小,

∵四边形ABCD是菱形,AC=6,DB=8,
∴OA=3,OB=4,AC⊥BD,
在Rt△AOB中,AB=![]() =5,
=5,
∵S菱形ABCD=![]() ,
,
∴![]() ,
,
∴NQ=![]() ,
,
∴PM+PN的最小值为![]() ,
,
故选D.
-
科目: 来源: 题型:
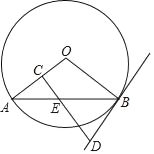
查看答案和解析>>【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为拓宽销售渠道,某水果商店计划将146个柚子和400个橙子装入大、小两种礼箱进行出售,其中每件小礼箱装2个柚子和4个橙子;每件大礼箱装3个柚子和9个橙子.要求每件礼箱都装满,柚子恰好全部装完,橙子有剩余,设小礼箱的数量为x件.
(1)大礼箱的数量为________件(用含x的代数式表示).
(2)若橙子剩余12个,则需要大、小两种礼箱共多少件?
(3)由于橙子有剩余,则小礼箱至少需要________件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从左至右第1个图由1个正六边形,6个正方形和6个等边三角形组成;第二个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成按此规律,第
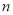 个图中正方形和等边三角形的个数之和为( )
个图中正方形和等边三角形的个数之和为( )
A.
 个B.
个B.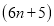 个C.
个C.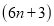 个D.
个D.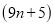 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠ADC=90°,AD=4cm,CD=3cm,AB=13cm,BC=12cm,求这个四边形的面积?
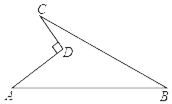
-
科目: 来源: 题型:
查看答案和解析>>【题目】1930年,德国汉堡大学的学生考拉兹,曾经提出过这样一个数学猜想:对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能够得到1.这一猜想后来成为著名的“考拉兹猜想”,又称“奇偶归一猜想”.虽然这个结论在数学上还没有得到证明,但举例验证都是正确的,例如:取正整数5,最少经过下面5步运算可得1,即:
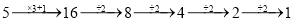 如果正整数
如果正整数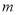 最少经过6步运算可得到1,则
最少经过6步运算可得到1,则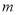 的值为__________.
的值为__________.
相关试题

