【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
参考答案:
【答案】(1)y=-![]() x2+24x+3200;
x2+24x+3200;
(2)每台冰箱应降价200元;
(3)每台冰箱的售价降价150元时,商场的利润最大,最大利润是5000元.
【解析】试题分析:(1)、根据总利润=单件利润×数量得出函数关系式;(2)、根据题意得出方程,然后进行求解;(3)、将二次函数配方成顶点式,然后进行计算.
试题解析:(1)、根据题意,得y=(2400-2000-x)(8+4×![]() ), 即y=-
), 即y=-![]() +24x+3200.
+24x+3200.
(2)、由题意,得-![]() +24x+3200=4800.整理,得
+24x+3200=4800.整理,得![]() -300x+20000=0.解这个方程,得
-300x+20000=0.解这个方程,得![]() =100,
=100, ![]() =200.
=200.
要使百姓得到实惠,取x=200.所以,每台冰箱应降价200元.
(3)、对于y=-![]() +24x+3200=-
+24x+3200=-![]() +5000,
+5000,
∴每台冰箱的售价降价150元时,商场的利润最大,最大利润是5000元
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列式子:1⊕3=1×2+3=5,3⊕1=3×2+1=7,5⊕4=5×2+4=14.请你想一想:(a﹣b)⊕(a+b)=_____.(用含a,b的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出几个多项式:①x2+y2;②﹣x2+y2;③x2+2xy+y2;④x4﹣1.其中能够分解因式的是__(填上序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=a,AD=b,E,F分别是AB,CD的中点,M是BC上一动点,AM,DM分别交EF于点G,H,连接CH.
(1)试判断GH是否为定值,并证明你的结论;
(2)当点M为BC的中点时,求证:四边形GMCH是平行四边形;
(3)试探究:在(2)的条件下,当a,b满足什么数量关系时,四边形GMCH是菱形?(不必证明,直接写出结论)
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程2x+3=7的解是( )
A.x=5
B.x=4
C.x=3.5
D.x=2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC约为多少米?( sin42°≈0.7,tan42°≈0.9)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE∥BF,先按(1)的要求作图,再按(2)的要求证明
(1)用直尺和圆规作出∠ABF的平分线BD交AE于点D,连接BD,再作出BD的中点O(不写作法,保留作图痕迹)
(2)连接(1)所作图中的AO并延长与BE相交于点C,连接DC,求证:四边形ABCD是菱形.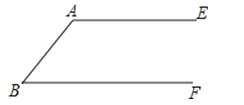
相关试题

