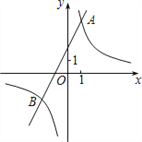
【题目】如图,已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2)。
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2)。
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1<y2成立的自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积。
参考答案:
【答案】(1)![]() ,
,![]() ;(2)-2<x<0或x>1;(3)12
;(2)-2<x<0或x>1;(3)12
【解析】分析:(1)先根据点A的坐标求出反比例函数的解析式为y1=![]() ,再求出B的坐标是(-2,-2),利用待定系数法求一次函数的解析式;
,再求出B的坐标是(-2,-2),利用待定系数法求一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直线在双曲线的下方,直接根据图象写出一次函数的值小于反比例函数的值x的取值范围x<-2 或0<x<1;
(3)根据坐标与线段的转换可得出:AC、BD的长,然后根据三角形的面积公式即可求出答案.
详解:(1)∵函数y1=![]() 的图象过点A(1,4),即4=
的图象过点A(1,4),即4=![]() ,
,
∴k=4,即y1=![]() ,
,
又∵点B(m,-2)在y1=![]() 上,
上,
∴m=-2,
∴B(-2,-2),
又∵一次函数y2=ax+b过A、B两点,
即![]() ,解之得
,解之得![]() .
.
∴y2=2x+2.
综上可得y1=![]() ,y2=2x+2;
,y2=2x+2;
(2)要使y1<y2,即函数y1的图象总在函数y2的图象下方,
∴-2<x<0或x>1.
(3)如图:
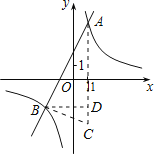
由图形及题意可得:AC=8,BD=3,
∴△ABC的面积S△ABC=![]() AC×BD=
AC×BD=![]() ×8×3=12.
×8×3=12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,在矩形ABCD中,E,F为BC上两点,且BE=CF,连接AF,DE交于点O.
求证:(1)△ABF≌△DCE;
(2)△AOD是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,在正方形ABCD中,AB=1,
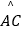 是以点B为圆心,AB长为半径的圆的一段弧,点E是边AD上的动点(点E与点A,D不重合),过E作
是以点B为圆心,AB长为半径的圆的一段弧,点E是边AD上的动点(点E与点A,D不重合),过E作 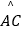 所在圆的切线,交边DC于点F,G为切点.
所在圆的切线,交边DC于点F,G为切点. 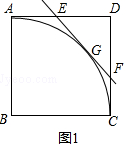
(1)求证:EA=EG;
(2)设AE=x,FC=y,求y关于x的函数关系式,并直接写出x的取值范围;
(3)如图2所示,将△DEF沿直线EF翻折后得△D1EF,连接AD1 , D1D,试探索:当点E运动到何处时,△AD1D与△ED1F相似?请说明理由.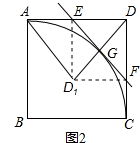
-
科目: 来源: 题型:
查看答案和解析>>【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的(探究).
(提出问题)两个有理数a、b满足a、b同号,求
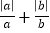 的值.
的值.(解决问题)解:由a、b同号,可知a、b有两种可能:①当a,b都正数;②当a,b都是负数.①若a、b都是正数,即a>0,b>0,有|a|=a,|b|=b,则
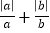 =
=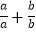 =1+1=2;②若a、b都是负数,即a<0,b<0,有|a|=﹣a,|b|=﹣b,则
=1+1=2;②若a、b都是负数,即a<0,b<0,有|a|=﹣a,|b|=﹣b,则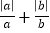 =
= =(﹣1)+(﹣1)=﹣2,所以
=(﹣1)+(﹣1)=﹣2,所以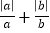 的值为2或﹣2.
的值为2或﹣2.(探究)请根据上面的解题思路解答下面的问题:
(1)两个有理数a、b满足a、b异号,求
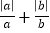 的值;
的值;(2)已知|a|=3,|b|=7,且a<b,求a+b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字0所对应的点与数轴上的数-2所对应的点重合,再让圆沿着数轴按顺时针方向滚动,那么数轴上的数-2017将与圆周上的哪个数字重合( )
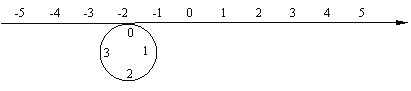
A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形ABCD为正方形,已知点A(﹣6,0),D(﹣7,3),点B、C在第二象限内.
(1)求点B的坐标。
(2)将正方形ABCD以每秒1个单位的速度沿x轴向右平移t秒,若存在某一时刻t,使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图象上,请求出此时t的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在x轴上的点P和反比例函数图象上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点P、Q的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD中,∠ABC的角平分线BE将边AD分成长度为5cm和6cm的两部分,则平行四边形ABCD的周长为__________________cm.
相关试题

