【题目】如图1所示,在正方形ABCD中,AB=1, ![]() 是以点B为圆心,AB长为半径的圆的一段弧,点E是边AD上的动点(点E与点A,D不重合),过E作
是以点B为圆心,AB长为半径的圆的一段弧,点E是边AD上的动点(点E与点A,D不重合),过E作 ![]() 所在圆的切线,交边DC于点F,G为切点.
所在圆的切线,交边DC于点F,G为切点. 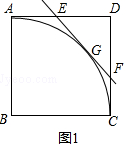
(1)求证:EA=EG;
(2)设AE=x,FC=y,求y关于x的函数关系式,并直接写出x的取值范围;
(3)如图2所示,将△DEF沿直线EF翻折后得△D1EF,连接AD1 , D1D,试探索:当点E运动到何处时,△AD1D与△ED1F相似?请说明理由. 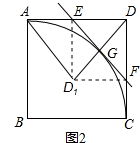
参考答案:
【答案】
(1)证明:∵四边形ABCD是正方形,
∴∠BAD=∠D=90°,AD=CD=AB=1,
∴AD⊥BA,
∴AD是圆B的切线,
∵EG是圆B的切线,
∴EA=EG
(2)解:∵EF切圆B于点G,
∴EA=EG,FC=FG.
∵AE=x,FC=y
∴EF=x+y,DE=1﹣x,DF=1﹣y,
在Rt△DEF中,根据勾股定理,得:(x+y)2=(1﹣x)2+(1﹣y)2
∴y= ![]() (0<x<1)
(0<x<1)
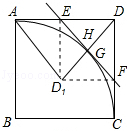
(3)解:当点E运动到AD的中点时,△AD1D与△ED1F相似;理由如下:
设直线EF交线段DD1于点H,由题意,得:
△EDF≌△ED1F,EF⊥DD1且DH=D1H.
∵AE= ![]() ,AD=1,
,AD=1,
∴AE=ED.
∴EH∥AD1,∠AD1D=∠EHD=90°.
又∵∠ED1F=∠EDF=90°,
∴∠FD1D=∠AD1D.
∴D1F∥AD,
∴∠ADD1=∠DD1F=∠EFD=45°,
∴△ED1F∽△AD1D.
【解析】(1)证出AD是圆B的切线,由切线长定理即可得出结论;(2)根据切线长定理、正方形的性质得到有关的线段用x,y表示,再根据勾股定理建立函数关系式.(3)根据切线长定理找到角之间的关系,从而发现正方形,根据正方形的性质得到两个角对应相等,从而证明三角形相似.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“2018东台西溪半程马拉松”的赛事共有两项:A、“半程马拉松”、 B、“欢乐跑”。小明参加了该项赛事的志愿者服务工作, 组委会随机将志愿者分配到两个项目组.
(1)小明被分配到“半程马拉松”项目组的概率为________.
(2)为估算本次赛事参加“半程马拉松”的人数,小明对部分参赛选手作如下调查:
调查总人数
20
50
100
200
500
参加“半程马拉松”人数
15
33
72
139
356
参加“半程马拉松”频率
0.750
0.660
0.720
0.695
0.712
①请估算本次赛事参加“半程马拉松”人数的概率为_______.(精确到0.1)
②若本次参赛选手大约有3000人,请你估计参加“半程马拉松”的人数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读)|4﹣1|表示4与1差的绝对值,也可以理解为4与1两数在数轴上所对应的两点之间的距离;|4+1|可以看做|4﹣(﹣1)|,表示4与﹣1的差的绝对值,也可以理解为4与﹣1两数在数轴上所对应的两点间的距离.
(1)|4﹣(﹣1)|=
(2)|5+2|=

(3)利用数轴找出所有符合条件的整数x,使得|x+3|=5,则x= .
(4)利用数轴找出所有符合条件的整数x,使得|x+3|+|x﹣2|=5,这样的整数是: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,在矩形ABCD中,E,F为BC上两点,且BE=CF,连接AF,DE交于点O.
求证:(1)△ABF≌△DCE;
(2)△AOD是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的(探究).
(提出问题)两个有理数a、b满足a、b同号,求
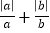 的值.
的值.(解决问题)解:由a、b同号,可知a、b有两种可能:①当a,b都正数;②当a,b都是负数.①若a、b都是正数,即a>0,b>0,有|a|=a,|b|=b,则
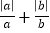 =
=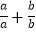 =1+1=2;②若a、b都是负数,即a<0,b<0,有|a|=﹣a,|b|=﹣b,则
=1+1=2;②若a、b都是负数,即a<0,b<0,有|a|=﹣a,|b|=﹣b,则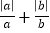 =
= =(﹣1)+(﹣1)=﹣2,所以
=(﹣1)+(﹣1)=﹣2,所以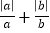 的值为2或﹣2.
的值为2或﹣2.(探究)请根据上面的解题思路解答下面的问题:
(1)两个有理数a、b满足a、b异号,求
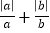 的值;
的值;(2)已知|a|=3,|b|=7,且a<b,求a+b的值.
-
科目: 来源: 题型:
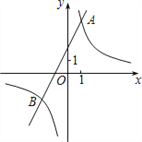
查看答案和解析>>【题目】如图,已知反比例函数y1=
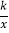 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2)。
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2)。(1)求这两个函数的关系式;
(2)观察图象,写出使得y1<y2成立的自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字0所对应的点与数轴上的数-2所对应的点重合,再让圆沿着数轴按顺时针方向滚动,那么数轴上的数-2017将与圆周上的哪个数字重合( )
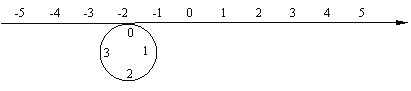
A. 0 B. 1 C. 2 D. 3
相关试题

