【题目】如图，在平面直角坐标系xOy中，抛物线y=x2+与y轴相交于点A，点B与点O关于点A对称

（1）填空：点B的坐标是 ；

（2）过点B的直线y=kx+b（其中k＜0）与x轴相交于点C，过点C作直线l平行于y轴，P是直线l上一点，且PB=PC，求线段PB的长（用含k的式子表示），并判断点P是否在抛物线上，说明理由；

（3）在（2）的条件下，若点C关于直线BP的对称点C′恰好落在该抛物线的对称轴上，求此时点P的坐标．

参考答案：

【答案】（1）（0，）；（2）点P在抛物线上,理由详见解析；（3）P点坐标为（，1）．

【解析】试题分析：（1）由抛物线解析式可求得点A的坐标，再利用对称可求得B点坐标；（2）可先用k表示出C点坐标，过B作BD⊥l于点D，条件可知P点在x轴上方，设P点纵坐标为y，可表示出PD、PB的长，在Rt△PBD中，利用勾股定理可求得y，则可求出PB的长，此时可得出P点坐标，代入抛物线解析式可判断P点在抛物线上；（3）利用平行线和轴对称的性质可得到∠OBC=∠CBP=∠C′BP=60°，则可求得OC的长，代入抛物线解析式可求得P点坐标．

试题解析：（1）∵抛物线y=x2+与y轴相交于点A，

∴A（0，），

∵点B与点O关于点A对称，

∴BA=OA=，

∴OB=，即B点坐标为（0，），

故答案为：（0，）；

（2）∵B点坐标为（0，），

∴直线解析式为y=kx+，令y=0可得kx+=0，解得x=﹣，

∴OC=﹣，

∵PB=PC，

∴点P只能在x轴上方，

如图1，过B作BD⊥l于点D，设PB=PC=m，

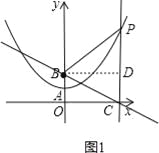
则BD=OC=﹣，CD=OB=，

∴PD=PC﹣CD=m﹣，

在Rt△PBD中，由勾股定理可得PB2=PD2+BD2，

即m2=（m﹣）2+（﹣）2，解得m=+，

∴PB=+，

∴P点坐标为（﹣，+），

当x=﹣时，代入抛物线解析式可得y=+，

∴点P在抛物线上；

（3）如图2，连接CC′，

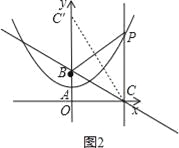
∵l∥y轴，

∴∠OBC=∠PCB，

又PB=PC，

∴∠PCB=∠PBC，

∴∠PBC=∠OBC，

又C、C′关于BP对称，且C′在抛物线的对称轴上，即在y轴上，

∴∠PBC=∠PBC′，

∴∠OBC=∠CBP=∠C′BP=60°，

在Rt△OBC中，OB=，则BC=1

∴OC=，即P点的横坐标为，代入抛物线解析式可得y=（）2+=1，

∴P点坐标为（，1）．

关闭