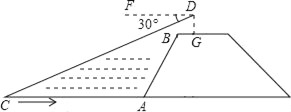
【题目】如图,小华站在河岸上的G点,看见河里有一小船沿垂直于岸边的方向划过来.此时测得小船C的俯角是∠FDC=30°.若小华的眼睛与地面的距离是![]() 米,BG=1.5米,BG平行于AC所在的直线,迎水坡i=4:3,坡长AB=10米,点A、B、C、D、F、G在同一平面内,则此时小船C到岸边的距离CA的长是多少?(结果保留根号)
米,BG=1.5米,BG平行于AC所在的直线,迎水坡i=4:3,坡长AB=10米,点A、B、C、D、F、G在同一平面内,则此时小船C到岸边的距离CA的长是多少?(结果保留根号)
参考答案:
【答案】CA的长约是(8![]() ﹣4.5)米.
﹣4.5)米.
【解析】试题分析:过点B作BE⊥AC于点E,延长DG交CA于点H,根据迎水坡AB的坡度i=4:3,坡长AB=10米,得出DH,CH的长,进而利用tan∠DCH=![]() =tan30°,求出CA即可.
=tan30°,求出CA即可.
试题解析:过点B作BE⊥AC于点E,延长DG交CA于点H,得Rt△ABE和矩形BEHG.
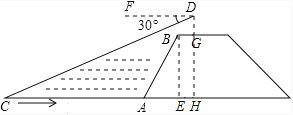
∵i=![]() ,AB=10米,
,AB=10米,
∴BE=8,AE=6.
∵DG=![]() ,BG=1.5,
,BG=1.5,
∴DH=DG+GH=![]() +8,
+8,
AH=AE+EH=6+1.5=7.5.
在Rt△CDH中,
∵∠C=∠FDC=30°,DH=8+![]() ,tan30°=
,tan30°=![]() ,
,
∴CH=8![]() +3.
+3.
又∵CH=CA+7.5,
即8![]() +3=CA+7.5,
+3=CA+7.5,
∴CA=8![]() ﹣4.5(米).
﹣4.5(米).
答:CA的长约是(8![]() ﹣4.5)米.
﹣4.5)米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=
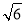 .现将△DEF与△ABC按如图所示的方式叠放在一起,使△ABC保持不动,△DEF运动,且满足点E在边BC上运动(不与B,C重合),边DE始终经过点A,EF与AC交于点M.在△DEF运动过程中,若△AEM能构成等腰三角形,则BE的长为______.
.现将△DEF与△ABC按如图所示的方式叠放在一起,使△ABC保持不动,△DEF运动,且满足点E在边BC上运动(不与B,C重合),边DE始终经过点A,EF与AC交于点M.在△DEF运动过程中,若△AEM能构成等腰三角形,则BE的长为______.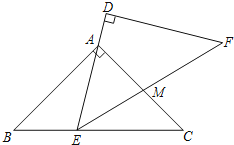
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
(1)则样本容量是 ,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天里发言次数不少于12的次数;
(3)已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.
发言次数n
A
0≤n<3
B
3≤n<6
C
6≤n<9
D
9≤n<12
E
12≤n<15
F
15≤n<18

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BE是△ABC的高,AE=BE,若要运用“HL”说明△AEF≌△BEC,还需添加条件:_________;若要运用“SAS”说明△AEF≌△BEC,还需添加条件:___________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1. 5倍.设两人出发x min后距出发点的距离为y m.图中折线段OBA表示小明在整个训练中y与x的函数关系,其中点A在x轴上,点B坐标为(2,480).
(1)点B所表示的实际意义是 ;
(2)求出AB所在直线的函数关系式;
(3)如果小刚上坡平均速度是小明上坡平均速度的一半,那么两人出发后多长时间第一次相遇?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长,与BC的延长线交于点F.
(1)求证:BD=BF;
(2)若BC=6,AD=4,求sinA的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.
(1)求A点坐标及线段AB的长;
(2)若点P由点A出发以每秒1个单位的速度沿AB边向点B移动,1秒后点Q也由点A出发以每秒7个单位的速度沿A-O-C-B的方向向点B移动,当其中一个点到达终点时另一个点也停止移动,点P的移动时间为t秒.
①当PQ⊥AC时,求t的值;
②当PQ∥AC时,对于抛物线对称轴上一点H,当点H的纵坐标满足条件_________时,∠HOQ<∠POQ.(直接写出答案)

相关试题

