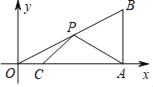
【题目】如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,顶点B的坐标为(3,![]() ),点C的坐标为(1,0),且∠B=60°,点P为斜边OB上的一个动点,则PA+PC的最小值为_____.
),点C的坐标为(1,0),且∠B=60°,点P为斜边OB上的一个动点,则PA+PC的最小值为_____.
参考答案:
【答案】![]()
【解析】
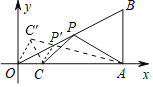
如图作点C关于直线OB的对称点C′,连接OC′,CC′,AC′,AC′交OB于P′,连接P′C,此时P′A+P′C的值最小,最小值为线段AC′的长.
如图作点C关于直线OB的对称点C′,连接OC′,CC′,AC′,AC′交OB于P′,连接P′C,此时P′A+P′C的值最小,最小值为线段AC′的长.
在Rt△OAB中,∵OA=3,AB=![]() ,
,
∴tan∠BOA=![]() ,
,
∴∠BOA=30°,
根据对称性可知:∠COC′=60°,OC=OC′=1,
∴△OCC′是等边三角形,
∴C′(![]() ,
,![]() ),
),
∵A(3,0),
∴AC′=![]() =
=![]() ,
,
∴PA+PC的最小值为![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=AD,BC=DC,∠A=90°,∠ABC=105°.若AB=5
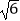 ,则△ABD外心与△BCD外心的距离为何?( )
,则△ABD外心与△BCD外心的距离为何?( ) 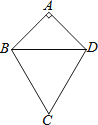
A.5
B.5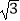
C.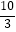
D.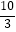
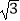

-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后分别按原速同时驶往甲地,两车之间的距离s(km)与慢车行驶时间t(h)之间的函数图象如图所示,则下列说法中:①甲、乙两地之间的距离为560km;②快车速度是慢车速度的1.5倍;③快车到达甲地时,慢车距离甲地60km;④相遇时,快车距甲地320km;正确的是( )
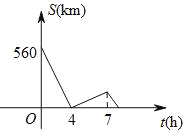
A. ①② B. ①③ C. ①④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,坐标平面上,二次函数y=﹣x2+4x﹣k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )

A.1
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具商店销售功能相同的两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需122元。
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B品牌计算器5个以上超出部分按原价的七折销售。设购买个x个A品牌的计算器需要y1元,购买x个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
(3)小明准备联系一部分同学集体购买同一品牌的计算器,若购买计算器的数量超过5个,购买哪种品牌的计算器更合算?请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为何?( )
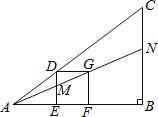
A.
B.
C.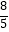
D.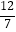
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1为长方形纸片ABCD,AD=26,AB=22,直线L、M皆为长方形的对称轴.今将长方形纸片沿着L对折后,再沿着M对折,并将对折后的纸片左上角剪下直角三角形,形成一个五边形EFGHI,如图2.最后将图2的五边形展开后形成一个八边形,如图2,且八边形的每一边长恰好均相等.
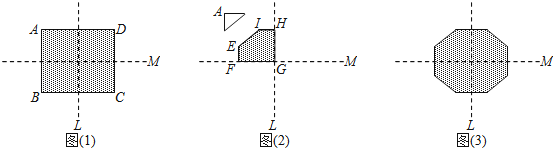
(1)若图2中HI长度为x,请以x分别表示剪下的直角三角形的勾长和股长.
(2)请求出图3中八边形的一边长的数值,并写出完整的解题过程.
相关试题

