【题目】图1为长方形纸片ABCD,AD=26,AB=22,直线L、M皆为长方形的对称轴.今将长方形纸片沿着L对折后,再沿着M对折,并将对折后的纸片左上角剪下直角三角形,形成一个五边形EFGHI,如图2.最后将图2的五边形展开后形成一个八边形,如图2,且八边形的每一边长恰好均相等.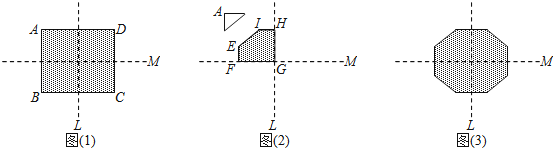
(1)若图2中HI长度为x,请以x分别表示剪下的直角三角形的勾长和股长.
(2)请求出图3中八边形的一边长的数值,并写出完整的解题过程.
参考答案:
【答案】
(1)
解:延长HI与FE相交于点N,如图所示.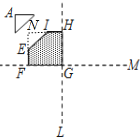
∵HN= ![]() AD=13,NF=
AD=13,NF= ![]() AB=11,HI=EF=x,
AB=11,HI=EF=x,
∴NI=HN﹣HI=13﹣x,NE=NF﹣EF=11﹣x,
∴剪下的直角三角形的勾长为11﹣x,股长为13﹣x
(2)
解:在Rt△ENI中,NI=13﹣x,NE=11﹣x,
∴EI= ![]() =
= ![]() .
.
∵八边形的每一边长恰好均相等,
∴EI=2HI=2x= ![]() ,
,
解得:x=5,或x=﹣29(舍去).
∴EI=2×5=10.
故八边形的边长为10
【解析】(1)延长HI与FE相交于点N,根据折叠的性质找出HN、NF的长,再根据边与边之间的关系即可求出NI、NE的长度,由此即可得出剪下的直角三角形的勾长与股长;
(2)结合(1)的结论利用勾股定理得出线段EI的长,再根据正八边形的性质即可列出关于x的方程,解方程即可得出结论.本题考查了翻折变换中的折叠问题、勾股定理以及解无理方程,解题的关键是:(1)根据边与边之间的关系计算出线段NI、NE的长;(2)列出关于x的无理方程.本题属于基础题,难度不大,解决该题型题目时,巧妙的利用勾股定理列出关于x的方程是关键.
【考点精析】利用翻折变换(折叠问题)对题目进行判断即可得到答案,需要熟知折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,顶点B的坐标为(3,
 ),点C的坐标为(1,0),且∠B=60°,点P为斜边OB上的一个动点,则PA+PC的最小值为_____.
),点C的坐标为(1,0),且∠B=60°,点P为斜边OB上的一个动点,则PA+PC的最小值为_____.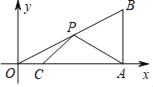
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具商店销售功能相同的两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需122元。
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B品牌计算器5个以上超出部分按原价的七折销售。设购买个x个A品牌的计算器需要y1元,购买x个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
(3)小明准备联系一部分同学集体购买同一品牌的计算器,若购买计算器的数量超过5个,购买哪种品牌的计算器更合算?请说明理由。
-
科目: 来源: 题型:
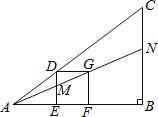
查看答案和解析>>【题目】如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为何?( )
A.
B.
C.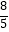
D.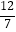
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D为AB上一点.已知△ADC与△DBC的面积比为1:3,且AD=3,AC=6,请求出BD的长度,并完整说明为何∠ACD=∠B的理由.
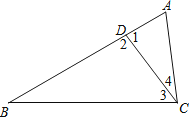
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+2与x轴、y轴分别交于A、B两点,OA:OB=
 .以线段AB为边在第二象限内作等腰Rt△ABC,∠BAC=90°.
.以线段AB为边在第二象限内作等腰Rt△ABC,∠BAC=90°.(1)求点A的坐标和k的值;
(2)求点C坐标;
(3)直线y=
 x在第一象限内的图象上是否存在点P,使得△ABP的面积与△ABC的面积相等?如果存在,求出点P坐标;如果不存在,请说明理由.
x在第一象限内的图象上是否存在点P,使得△ABP的面积与△ABC的面积相等?如果存在,求出点P坐标;如果不存在,请说明理由.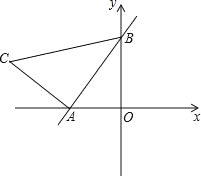
-
科目: 来源: 题型:
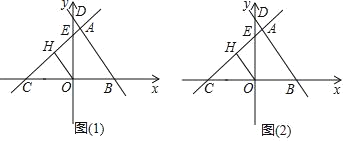
查看答案和解析>>【题目】如图(1),平面直角坐标系中,直线y=
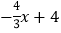 与x轴、y轴分别交于点B、D,直线y=
与x轴、y轴分别交于点B、D,直线y=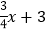 与x轴、y轴分别交于点C、E,且两条直线交于点A.
与x轴、y轴分别交于点C、E,且两条直线交于点A.(1)若OH⊥CE于点H,求OH的长.
(2)求四边形ABOE的面积.
(3)如图(2),已知点F(﹣
 ,0),在△ABC的边上取两点M、N,是否存在以点O,M,N为顶点的三角形与△OFM全等,且两个三角形在边OM的异侧?若存在,请直接写出所有符合条件的点M的坐标,若不存在,请说明理由.(温馨提示:若点A(x1,y1),点B(x2,y2),则线段AB的中点坐标为(
,0),在△ABC的边上取两点M、N,是否存在以点O,M,N为顶点的三角形与△OFM全等,且两个三角形在边OM的异侧?若存在,请直接写出所有符合条件的点M的坐标,若不存在,请说明理由.(温馨提示:若点A(x1,y1),点B(x2,y2),则线段AB的中点坐标为( ,
,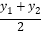 ).
).
相关试题

