【题目】如图,在△ABC中,∠C=90°, AD平分∠BAC交BC于D,DE⊥AB于E
求证:(1)△ACD≌△AED;(2)若AB=6,求△DEB的周长。

参考答案:
【答案】(1)证明见解析;(2)6
【解析】试题分析:(1)根据角平分线性质求出CD=DE,根据HL定理求出两三角形全等即可;
(2)根据全等三角形的性质得到AC=AE,CD=DE,由于AC=BC,等量代换得到BC=AE,于是得到△DEB的周长=DB+DE+EB=DB+CD+EB=CB+BE=AE+BE=6.
试题解析:(1)∵AD平分∠CAB,DE⊥AB,∠C=90,
∴CD=ED,∠DEA=∠C=90,
在Rt△ACD和Rt△AED中,
![]() ,
,
∴Rt△ACD≌Rt△AED(HL);
(2)∵△ACD≌△AED,
∴AC=AE,CD=DE,
∵AC=BC,
∴BC=AE,
∴△DEB的周长=DB+DE+EB=DB+CD+EB=CB+BE=AE+BE=AB=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2004年4月我国铁路第5次大提速。假设Kl20次空调快速列车的平均速度提速后比提速前提高了44千米/时,提速前的列车时刻表如下:
行驶区间
车次
起始时刻
到站时刻
历时
全程里程
A地—B地
K120
2:00
6:00
4小时
264千米
请你根据题目提供的信息,填写提速后的列车时刻表,并写出计算过程。
行驶区间
车次
起始时刻
到站时刻
历时
全程里程
A地—B地
K120
2:00
264千米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.

(1)补全△A′B′C′,利用网格点和直尺画图;
(2)图中AC与A1C1的关系是:______;
(3)画出△ABC中AB边上的中线CE;
(4)平移过程中,线段AC扫过的面积是_________
-
科目: 来源: 题型:
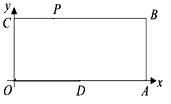
查看答案和解析>>【题目】已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上以每秒1个单位的速度由C向B运动。
(1) 求梯形ODPC的面积S与时间t的函数关系式。
(2) t为何值时,四边形PODB是平行四边形?
(3) 在线段PB上是否存在一点Q,使得ODQP为菱形。若存在求t值,若不存在,说明理由。
(4) 当△OPD为等腰三角形时,求点P的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=
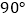 ,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
A. 1个
B. 2个
C. 3个
D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国政府从2007年起对职业中专在校生给予生活补贴,每位在校生每年补贴1500元某市预计2008年职业中专在校生人数是2007年的1.2倍,于是要在2007年的基础上增加补贴600万元。2008年该市职业中专在校生有多少万人?补贴多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
(1)求证:AD=CE;
(2)求∠DFC的度数.

相关试题

