【题目】如图,四边形ABCD中,AC、BD是它的对角线,∠ABC=∠ADC=90°,∠BCD是锐角.
(1)若BD=BC,证明:sin∠BCD=![]() .
.
(2)若AB=BC=4,AD+CD=6,求![]() 的值.
的值.
(3)若BD=CD,AB=6,BC=8,求sin∠BCD的值.
(注:本题可根据需要自己画图并解答)
参考答案:
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】分析:
(1)如图1,过点B作BE⊥AD交AD的延长线于点E,由已知条件易得点A、B、C、D四点共圆,由此可得∠EAB=∠BCD,∠EDB=∠BCA,结合∠DEB=∠ABC=90°,可得△BED∽△ABC,从而可得sin∠BCD=sin∠EAB=![]() ,结合BD=BC即可得到所求结论;
,结合BD=BC即可得到所求结论;
(2)如图2中,过点B作BF⊥BD交DC的延长线于F.由已知条件通过证△DAB≌△CBF得到BD=BF,AD=CF,从而可得△DBF是等腰直角三角形,由此可得BD=![]() DF,结合DF=DC+CF=DC+AD=6即可求得BD的长,在Rt△ABC中求得AC的长即可求得
DF,结合DF=DC+CF=DC+AD=6即可求得BD的长,在Rt△ABC中求得AC的长即可求得![]() 的值;
的值;
(3)当BD=CD时,如图3中,过点B作MN∥DC,过点C作CN⊥MN,垂足为N,延长DA交MN于点M,易得四边形DCNM是矩形,△ABM∽△BCN,从而可得![]() ,设AM=6y,BN=8y,BM=6x,CN=8x,则易得BD=10x,由BD=DC=MN=MB+BN可得10x=6x+8y,则x=2y,由此在Rt△ABM中,可得AB=
,设AM=6y,BN=8y,BM=6x,CN=8x,则易得BD=10x,由BD=DC=MN=MB+BN可得10x=6x+8y,则x=2y,由此在Rt△ABM中,可得AB=![]() =6
=6![]() y,结合(1)中所得∠BCD=∠MAB即可由sin∠MAB=
y,结合(1)中所得∠BCD=∠MAB即可由sin∠MAB=![]() 求得sin∠BCD的值了.
求得sin∠BCD的值了.
详解:
(1)如图1中,过点B作AD的垂线BE交DA的延长线于点E,
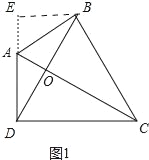
∵∠ABC=∠ADC=90°,
∴∠ADC+∠ABC=180°,
∴点A、B、C、D四点共圆,
∴∠BDE=∠ACB,∠EAB=∠BCD,
∵∠BED=∠ABC=90°,
∴△BED∽△ABC,
∴![]() ,
,
∵ ∠EAB=∠BCD,sin∠EAB=![]() ,
,
∴sin∠BCD=![]() ;
;
(2)如图2中,过点B作BF⊥BD交DC的延长线于F.
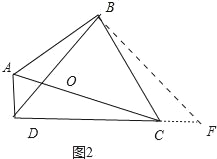
∵∠ABC=∠DBF=90°,∠BAD+∠BCD+∠ABC+∠ADC=360°,∠ABC+∠ADC=180°,
∴∠BAD=180°﹣∠BCD=∠BCF,
∵∠BCF=∠BAD,BC=BA,
∴△DAB≌△CBF,
∴BD=BF,AD=CF,
∵∠DBF=90°,
∴△BDF是等腰直角三角形,
∴BD=![]() DF,
DF,
∵AD+CD=6,
∴CF+CD=DF=6,
∴BD=3![]() ,AC=
,AC=![]() ,
,
∴![]() .
.
(3)当BD=CD时,如图3中,过点B作MN∥DC,过点C作CN⊥MN,垂足为N,延长DA交MN于点M,则四边形DCNM是矩形,△ABM∽△BCN,
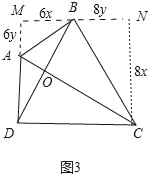
∴![]() ,
,
设AM=6y,BN=8y,BM=6x,CN=8x,
在Rt△BDM中,BD=![]() =10x,
=10x,
∵BD=DC,
∴10x=6x+8y,
∴x=2y,
在Rt△ABM中,AB=![]() =6
=6![]() y,
y,
∴sin∠BCD=sin∠MAB=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),∠BAO=30°.

(1)求AB的长度;
(2)以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点,求证:BD=OE;
(3)在(2)的条件下,连接DE交AB于F,求证:F为DE的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学对全校1200名学生进行“校园安全知识”的教育活动,从1200名学生中随机抽取部分学生进行测试,成绩评定按从高分到低分排列分为
 四个等级,绘制了图①、图②两幅不完整的统计图,请结合图中所给信息解答下列问题:
四个等级,绘制了图①、图②两幅不完整的统计图,请结合图中所给信息解答下列问题:
(1)求本次抽查的学生共有______人;
(2)将条形统计图和扇形统计图补充完整;
(3)扇形统计图中“
 ”所在扇形圆心角的度数为______;
”所在扇形圆心角的度数为______;(4)估计全校“
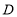 ”等级的学生有______人
”等级的学生有______人 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为﹣6,点B在数轴上A点右侧,且AB=14,动点M从点A出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.

(1)写出数轴上点B表示的数 ,点M表示的数 (用含t的式子表示);
(2)动点N从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点M,N同时出发,问点M运动多少秒时追上点N?
(3)若P为AM的中点,F为MB的中点,点M在运动过程中,线段PF的长度是否发生变化?若变化,请说明理由;若不变,请求出线段PF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴的单位长度为1.

(1)如果点B,D表示的数互为相反数,那么图中点A、点D表示的数分别是 、 ;
(2)当点B为原点时,在数轴上是否存在点M,使得点M到点A的距离是点M到点D的距离的2倍,若存在,请求出此时点M所表示的数;若不存在,说明理由;
(3) 在(2)的条件下,点A、点C分别以2个单位长度/秒和0.5个单位长度同时向右运动,同时点P从原点出发以3个单位长度/秒的速度向左运动,当点A与点C之间的距离为3个单位长度时,求点P所对应的数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下(x>6且x<14,单位:km):

(1)写出这辆出租车每次行驶的方向;
(2)求经过连续4次行驶后,这辆出租车所在的位置(结果可用x表示);
(3)这辆出租车一共行驶了多少路程(结果用x表示)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】长方形
 放置在如图所示的平面直角坐标系中,点
放置在如图所示的平面直角坐标系中,点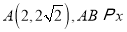 轴,
轴,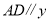 轴,
轴,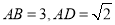 .
.(1)分别写出点
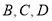 的坐标______;______;________.
的坐标______;______;________.(2)在
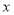 轴上是否存在点
轴上是否存在点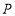 ,使三角形
,使三角形 的面积为长方形ABCD面积的
的面积为长方形ABCD面积的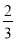 ?若存在,请直接写出点
?若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.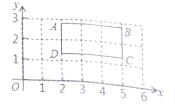
相关试题

