【题目】如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且CE=CD,试猜想BD和AE的关系,并说明你猜想的正确性.

参考答案:
【答案】猜想:BD=AE ,BD⊥AE.
【解析】
猜想:BD=AE ,BD⊥AE,先证明△BDC≌△AEC得出BD=AE,∠CBD=∠CAE,从而得出∠BFE=90°,即BF⊥AE.
解:猜想:BD=AE ,BD⊥AE.
理由:延长BD交AE于点F,
∵∠ACB=90°,
∴∠ACE=∠BCD=90°.

又BC=AC,CD=CE,
∴△BDC≌△AEC(HL).
∴BD=AE
∴∠CBD=∠CAE.
又∠CAE+∠E=90°.
∴∠EBF+∠E=90°.
∴∠BFE=90°,∴BF⊥AE,即BD⊥AE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD中,E是AC上一点,EF⊥AB , EG⊥AD , AB=6,AE:EC=2:1.求四边形AFEG的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题,真命题是( )

A.如图,如果OP平分∠AOB,那么,PA=PB
B.三角形的一个外角大于它的一个内角
C.如果两条直线没有公共点,那么这两条直线互相平行
D.有一组邻边相等的矩形是正方形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BD为△ABC的角平分线,请按如下要求操作解答:
(1)过点D画DE∥BC交AB于E,若∠A=68°,∠AED=42°,求∠BDC的度数.
(2)画△ABC的角平分线CF交BD于点M,若∠A=60°,求∠CMD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为
 的线段的概率为( )
的线段的概率为( ) 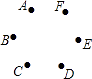
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )

A. =
= 
B.AD,AE将∠BAC三等分
C.△ABE≌△ACD
D.S△ADH=S△CEG -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC.延长AD到E点,使DE=AB.连接CE.求∠E的度数.

相关试题

