【题目】正方形ABCD中,E是AC上一点,EF⊥AB , EG⊥AD , AB=6,AE:EC=2:1.求四边形AFEG的面积.
参考答案:
【答案】解答:正方形ABCD中,∠DAB=90°,∠DAC=45°,
又∵∠AFE=∠AGE=90°,
∴四边形AFEG是矩形,∠AEG=90°-∠DAC=45°,
∴∠GAE=∠AEG=45°,
∴GE=AG ,
∴矩形AFEG是正方形,
∵四边形ABCD是正方形,
∴正方形AFEG∽正方形ABCD ,
∴ ![]() =(
=( ![]() )2=(
)2=( ![]() )2=
)2= ![]() ,
,
∴S正方形AFEG= ![]() S正方形AFEG=
S正方形AFEG= ![]() ×62=16.
×62=16.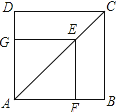
【解析】先证明四边形AFEG是正方形,再由相似的定义得出正方形AFEG∽正方形ABCD , 最后根据相似多边形的面积比等于相似比的平方进行求解.
【考点精析】掌握相似图形是解答本题的根本,需要知道形状相同,大小不一定相同(放大或缩小);判定:①平行;②两角相等;③两边对应成比例,夹角相等;④三边对应成比例.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果二次根式
 与
与  能够合并,能否由此确定a=1?若能,请说明理由;不能,请举一个反例说明.
能够合并,能否由此确定a=1?若能,请说明理由;不能,请举一个反例说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形ABCD中,AB=1,在BC上取一点E , 沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD=( ).

A.
B.
C.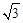
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形,矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.设菱形相邻两个内角的度数分别为m和n , 将菱形的“接近度”定义为|m-n|,于是,|m-n|越小,菱形越接近于正方形.若菱形的一个内角为70°,则该菱形的“接近度”等于;当菱形的“接近度”等于时,菱形是正方形.
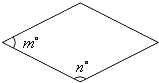
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题,真命题是( )

A.如图,如果OP平分∠AOB,那么,PA=PB
B.三角形的一个外角大于它的一个内角
C.如果两条直线没有公共点,那么这两条直线互相平行
D.有一组邻边相等的矩形是正方形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BD为△ABC的角平分线,请按如下要求操作解答:
(1)过点D画DE∥BC交AB于E,若∠A=68°,∠AED=42°,求∠BDC的度数.
(2)画△ABC的角平分线CF交BD于点M,若∠A=60°,求∠CMD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且CE=CD,试猜想BD和AE的关系,并说明你猜想的正确性.

相关试题

