【题目】如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC.延长AD到E点,使DE=AB.连接CE.求∠E的度数.

参考答案:
【答案】45°
【解析】
连接AC,首先根据四边形的内角和等于360°,结合已知条件求出∠ABC+∠ADC=180°,再利用同角的补角相等得到∠ABC=∠CDE,接下来依据“边角边”即可证得△ABC≌△EDC,再利用全等三角形的性质求解即可.
证明:在连接AC.
四边形ABCD中,∵∠BAD=∠BCD=90°,
∴∠ABC+∠ADC=180°,
又∵∠CDE+∠ADC=180°,
∴∠ABC=∠CDE,
在△ABC和△EDC中,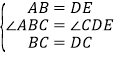 ,
,
∴△ABC≌△EDC(SAS),
∴∠BAC=∠CED,AC=EC,
∴∠EAC=∠CED,∴∠BAC=∠CAE=![]() ∠BAD=
∠BAD=![]() ,
,
∴∠AEC=![]() 即∠E=
即∠E=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且CE=CD,试猜想BD和AE的关系,并说明你猜想的正确性.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为
 的线段的概率为( )
的线段的概率为( ) 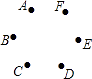
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )

A. =
= 
B.AD,AE将∠BAC三等分
C.△ABE≌△ACD
D.S△ADH=S△CEG -
科目: 来源: 题型:
查看答案和解析>>【题目】请按要求完成下面三道小题.
(1)如图1,AB=AC.这两条线段一定关于某条直线对称吗?如果是,请说明是哪条直线,并在图1中画出这条直线;如果不是,请说明理由.

(2)如图2,已知线段AB和点C.
求作线段CD,使它与AB成轴对称,且A与C是对称点,请画出图形,并简述画图过程.

(3)如图3,任意位置的两条线段AB,CD,AB=CD.你能通过对其中一条线段作有限次的轴对称使它们重合吗?如果能,请画出图形,并描述操作过程;如果不能,请说明理由.

-
科目: 来源: 题型:
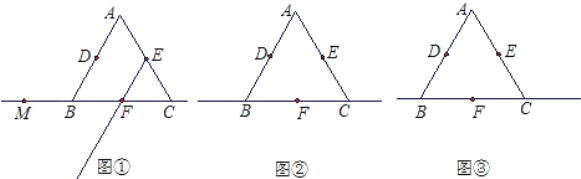
查看答案和解析>>【题目】如图:已知△ABC是等边三角形,D、E、F分别是AB、AC、BC边的中点,M是直线BC上的任意一点,在射线EF上截取EN,使EN=FM,连接DM、MN、DN.
(1)如图①,当点M在点B左侧时,请你按已知要求补全图形,并判断△DMN是怎样的特殊三角形(不要求证明);
(2)请借助图②解答:当点M在线段BF上(与点B、F不重合),其它条件不变时,(1)中的结论是否依然成立?若成立,请证明;若不成立,请说明理由;
(3)请借助图③解答:当点M在射线FC上(与点F不重合),其它条件不变时,(1)中的结论是否仍然成立?画出图形,不要求证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题,真命题是( )

A.如图,如果OP平分∠AOB,那么,PA=PB
B.三角形的一个外角大于它的一个内角
C.如果两条直线没有公共点,那么这两条直线互相平行
D.有一组邻边相等的矩形是正方形
相关试题

