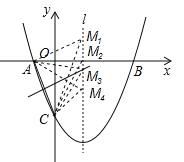
【题目】如图,已知抛物线![]() (a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.
(a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.

(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为等腰三角形,请直接写出所有符合条件的点M的坐标.
参考答案:
【答案】(1)![]() ;(2)P(1,0);(3).
;(2)P(1,0);(3).
【解析】
试题分析:(1)直接将A、B、C三点坐标代入抛物线的解析式中求出待定系数即可;
(2)由图知:A.B点关于抛物线的对称轴对称,那么根据抛物线的对称性以及两点之间线段最短可知,直线l与x轴的交点,即为符合条件的P点;
(3)由于△MAC的腰和底没有明确,因此要分三种情况来讨论:①MA=AC、②MA=MC、③AC=MC;可先设出M点的坐标,然后用M点纵坐标表示△MAC的三边长,再按上面的三种情况列式求解.
试题解析:(1)将A(﹣1,0)、B(3,0)、C(0,﹣3)代入抛物线![]() 中,得:
中,得: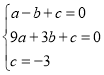 ,解得:
,解得: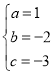 ,故抛物线的解析式:
,故抛物线的解析式:![]() .
.
(2)当P点在x轴上,P,A,B三点在一条直线上时,点P到点A、点B的距离之和最短,此时x=![]() =1,故P(1,0);
=1,故P(1,0);
(3)如图所示:抛物线的对称轴为:x=![]() =1,设M(1,m),已知A(﹣1,0)、C(0,﹣3),则:
=1,设M(1,m),已知A(﹣1,0)、C(0,﹣3),则:
![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,![]() =10;
=10;
①若MA=MC,则![]() ,得:
,得:![]() =
=![]() ,解得:m=﹣1;
,解得:m=﹣1;
②若MA=AC,则![]() ,得:
,得:![]() =10,得:m=
=10,得:m=![]() ;
;
③若MC=AC,则![]() ,得:
,得:![]() =10,得:
=10,得:![]() ,
,![]() ;
;
当m=﹣6时,M、A、C三点共线,构不成三角形,不合题意,故舍去;
综上可知,符合条件的M点,且坐标为 M(1,![]() )(1,
)(1,![]() )(1,﹣1)(1,0).
)(1,﹣1)(1,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】2014年12月10日,连通杭州、南昌、长沙三座省会城市的杭长高铁开通,这给勇于创业的衢州人民的出行带来了极大的方便.杭长高铁总投资1300亿元,1300亿元用科学记数法表示为( )
A.13×1010元
B.1.3×1010元
C.0.13×1012元
D.1.3×1011元 -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(m-n)(m+n)+(m+n)2-2m2,其中m=1,n=-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列成语描述的事件为随机事件的是( )
A.水涨船高
B.守株待兔
C.水中捞月
D.缘木求鱼 -
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )

A.20海里 B.40海里 C.
 海里 D.
海里 D. 海里
海里 -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个三角形中,各边和它所对角的正弦的比相等.即
 .利用上述结论可以求解如下题目.如:
.利用上述结论可以求解如下题目.如:在
 中,若∠A=45°,∠B=30°,a=6,求b.
中,若∠A=45°,∠B=30°,a=6,求b. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值= .

相关试题

