【题目】抛物线 y=x2+mx+n 过点(-1,8)和点(4,3)且与 x 轴交于 A,B 两点, 与 y 轴交于点 C
(1)求抛物线的解析式;
(2)如图1,AD 交抛物线于 D,交直线 BC 于点 G,且 AG=GD,求点 D 的坐标;
(3)如图2,过点 M(3,2)的直线交抛物线于 P,Q,AP 交 y 轴于点 E,AQ 交y 轴于点 F,求OE·OF的值.


参考答案:
【答案】(1)y=x2-4x+3;(2)D(![]() ,
,![]() )或(
)或(![]() ,
,![]() );(3)2.
);(3)2.
【解析】
(1)利用待定系数法求函数解析式即可;(2)先求得点A、B、C的坐标及直线BC的解析式,过点G作GR⊥x轴于点R,过点D作DK⊥x轴于点K(如图),由AG=GD,可得GR=![]() DK,设点D的坐标为(a,a2-4a+3),则点G的坐标为(
DK,设点D的坐标为(a,a2-4a+3),则点G的坐标为(![]() ,-
,-![]() +3),可得方程-
+3),可得方程-![]() +3=
+3=![]() (a2-4a+3),解方程求得a的值,即可得点D的坐标;(3)设AQ的解析式为y=ax-a,AP的解析式为y=bx-b,分别根抛物线的解析式联立,求得点P、Q的横坐标,在设PQ的解析式为y=kx+b,代入M(3,2)可得y=kx+2-3k. 将PQ的解析式为与抛物线解析式联立得到关于x的一元二次方程,然后依据一元二次方程根与系数的关系可求得ab=﹣2,再由ab的值可得到OEOF的值即可.
(a2-4a+3),解方程求得a的值,即可得点D的坐标;(3)设AQ的解析式为y=ax-a,AP的解析式为y=bx-b,分别根抛物线的解析式联立,求得点P、Q的横坐标,在设PQ的解析式为y=kx+b,代入M(3,2)可得y=kx+2-3k. 将PQ的解析式为与抛物线解析式联立得到关于x的一元二次方程,然后依据一元二次方程根与系数的关系可求得ab=﹣2,再由ab的值可得到OEOF的值即可.
(1)把点(-1,8)和点(4,3)代入y=x2+mx+n得,
![]() ,
,
解得![]() ,
,
∴y=x2-4x+3;
(2)令x2-4x+3=0,解得x=1或x=3,
∴A(1,0),B(3,0);
把x=0代入y=x2-4x+3得y=3,
∴C(0,3);
∴直线BC的解析式为y=-x+3.
如图,过点G作GR⊥x轴于点R,过点D作DK⊥x轴于点K,
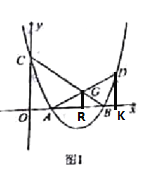
∴GR∥DK,
∵AG=GD,
∴GR=![]() DK,
DK,
设点D的坐标为(a,a2-4a+3),则点G的坐标为(![]() ,-
,-![]() +3),
+3),
即GR=-![]() +3,DK= a2-4a+3,
+3,DK= a2-4a+3,
∴-![]() +3=
+3=![]() (a2-4a+3),
(a2-4a+3),
整理得a2-3a-2=0,
解得,![]() ,
,![]() ,
,
∴D(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
(3)∵A(1,0),
设AQ的解析式为y=ax-a,AP的解析式为y=bx-b,
∴![]() ,解得x=1或x=a+3,
,解得x=1或x=a+3,
∴点Q的横坐标为a+3,
同理求得点P的横坐标为b+3.
设PQ的解析式为y=kx+b,把点 M(3,2)代入可得3k+b=2,即b=2-3k.
∴y=kx+2-3k.
∴kx+2-3k= x2-4x+3,即x2-(4+k)x+1+3k=0,
∵P、Q是抛物线y=x2-4x+3与直线PQ的交点,
∴a+3、b+3是方程x2-(4+k)x+1+3k=0的两个根,
∴a+3+b+3=4+k,(a+3)(b+3)=1+3k,
即a+b=k-2,ab+3(a+b)+9=1+3k,
∴ab+3(k-2)+9=1-3k,
整理得ab=-2,
∵OE=-b,OF=a,
∴OEOF=-ab=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B. C.E在同一条直线上,连结DC.

(1)请在图2中找出与△ABE全等的三角形,并给予证明;
(2)证明:DC⊥BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ ABC中,AB = AC

(1)如图 1,如果∠BAD = 30°,AD是BC上的高,AD =AE,则∠EDC =
(2)如图 2,如果∠BAD = 40°,AD是BC上的高,AD = AE,则∠EDC =
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:
(4)如图 3,如果AD不是BC上的高,AD = AE,是否仍有上述关系?如有,请你写出来,并说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,∠A=∠B=30°,E,F 在 AB 上,∠ECF=60°.
(1)画出△BCF 绕点 C 顺时针旋转 120°后的△ACK;
(2)在(1)中,若 AE2+ EF2= BF2,求证 BF=
 CF.
CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)阅读理解:
我们知道,只用直尺和圆规不能解决的三个经典的希腊问题之一是三等分任意角,但是这个任务可以借助如图1所示的一边上有刻度的勾尺完成,勾尺的直角顶点为P,
“宽臂”的宽度=PQ=QR=RS,(这个条件很重要哦!)勾尺的一边MN满足M,N,Q三点共线(所以PQ⊥MN).
下面以三等分∠ABC为例说明利用勾尺三等分锐角的过程:
第一步:画直线DE使DE∥BC,且这两条平行线的距离等于PQ;
第二步:移动勾尺到合适位置,使其顶点P落在DE上,使勾尺的MN边经过点B,同时让点R落在∠ABC的BA边上;
第三步:标记此时点Q和点P所在位置,作射线BQ和射线BP.
请完成第三步操作,图中∠ABC的三等分线是射线 、 .
(2)在(1)的条件下补全三等分∠ABC的主要证明过程:
∵ ,BQ⊥PR,
∴BP=BR.(线段垂直平分线上的点与这条线段两个端点的距离相等)
∴∠ =∠ .
∵PQ⊥MN,PT⊥BC,PT=PQ,
∴∠ =∠ .
(角的内部到角的两边距离相等的点在角的平分线上)
∴∠ =∠ =∠ .
(3)在(1)的条件下探究:
 是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出
是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出 (无需写画法,保留画图痕迹即可).
(无需写画法,保留画图痕迹即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售某种玩具,进货价为
 元.根据市场调查:在一段时间内,销售单价是
元.根据市场调查:在一段时间内,销售单价是 元时,销售量是
元时,销售量是 件,而销售单价每上涨
件,而销售单价每上涨 元,就会少售出
元,就会少售出 件玩具,超市要完成不少于
件玩具,超市要完成不少于 件的销售任务,又要获得最大利润,则销售单价应定为________元.
件的销售任务,又要获得最大利润,则销售单价应定为________元. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数的图象经过点
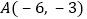 .
. 写出函数表达式;
写出函数表达式; 这个函数的图象在哪几个象限?
这个函数的图象在哪几个象限? 随
随 的增大怎样变化?
的增大怎样变化? 点
点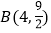 、
、 在这个函数的图象上吗?
在这个函数的图象上吗? 如果点
如果点 在图象上,求
在图象上,求 的值.
的值.
相关试题

