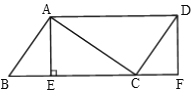
【题目】如图,在平行四边形ABCD中,AE⊥BC于E,点F在BC延长线上,且CF=BE,连接AC,DF,
(1)求证:四边形AEFD是矩形;
(2)若∠ACD=90°,CF=3,DF=4,求AD的长度.
参考答案:
【答案】(1)见详解;(2)![]()
【解析】
(1)由平行四边形的性质得AD=BC,AD∥BC,再由CF=BE证得AD=EF,进而可证矩形;
(2)先由CF=3,DF=4求得DC=5,再利用△ACD∽△DFC即可求得AD的长.
(1)证明:∵在平行四边形ABCD中,
∴AD=BC,AD∥BC,
∵CF=BE,
∴CF+CE=BE+CE,
即:BC=EF,
∴AD=EF,
又∵AD∥BC,
∴四边形AEFD为平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴平行四边形AEFD为矩形;
(2)解:∵在矩形AEFD中,
∴∠F=90°,
∵CF=3,DF=4,
∴在Rt△CDF中,CD=![]() ,
,
∵AD∥BC,
∴∠ADC=∠DCF,
又∵∠ACD=90°,
∴∠ACD=∠F,
∴△ACD∽△DFC
∴![]()
∴![]()
∴AD=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠PAQ=36°,点B为射线AQ上一固定点,按以下步骤作图:①分别以A,B为圆心,大于
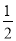 AB的长为半径画弧,相交于两点M,N;②作直线MN交射线AP 于点D,连接 BD;③以B为圆心,BA长为半径画弧,交射线AP 于点C; 根据以上作图过程及所作图形,下列结论中错误的是( )
AB的长为半径画弧,相交于两点M,N;②作直线MN交射线AP 于点D,连接 BD;③以B为圆心,BA长为半径画弧,交射线AP 于点C; 根据以上作图过程及所作图形,下列结论中错误的是( )
A.∠CDB=72°B.△ADB∽△ABCC.CD:AD=2:1D.∠ABC=3∠ACB
-
科目: 来源: 题型:
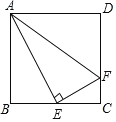
查看答案和解析>>【题目】如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF.有下列结论:①∠BAE=30°;②射线FE是∠AFC的角平分线;③AE2=ADAF;④AF=AB+CF.其中正确结论为是______.(填写所有正确结论的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是娜娜设计的“作一个角等于已知角”的尺规作图过程.
已知:RT△ABC,
求作:AB上作点D,使∠BCD=∠A.

作法:如图,以AC为直径作圆,交AB于D,所以点D就是所求作的点;
根据娜娜设计的作图过程,完成下面的证明.
证明:∵AC是直径
∴∠ADC=90°(______)(填推理的依据)
即∠ACD+∠A=90°,
∵∠ACB=90°,
即∠ACD+_______=90°,
∴∠BCD=∠A(_______)(填推理的依据).
-
科目: 来源: 题型:
查看答案和解析>>【题目】央视举办的《主持人大赛》受到广泛的关注.某中学学生会就《主持人大赛》节目的喜爱程度,在校内对部分学生进行了问卷调查,并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级,分别记作
 、
、 、
、 、
、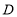 .根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中所给信息解答下列问题:
.根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中所给信息解答下列问题: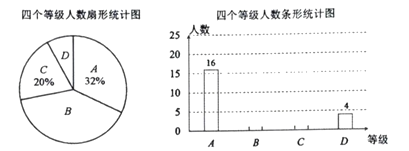
(1)本次被调查对象共有 人;扇形统计图中被调查者“比较喜欢”等级所对应圆心角的度数为 .
(2)将条形统计图补充完整,并标明数据;
(3)若选“不太喜欢”的人中有两个女生和两个男生,从选“不太喜欢”的人中挑选两个学生了解不太喜欢的原因,请用列举法(画树状图或列表),求所选取的这两名学生恰好是一男一女的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C 是⊙O上一点,过点C 作⊙O的切线,交BA的延长线交于点D,过点B 作BE⊥BA,交DC延长线于点E,连接OE,交⊙O于点F,交BC于点H,连接AC.
(1)求证:∠ECB=∠EBC;
(2)连接BF,CF,若BF=5,sin∠FBC=
 ,求AC的长.
,求AC的长. 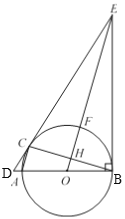
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,函数y=
 (x>0)的图象与直线y=
(x>0)的图象与直线y=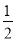 x+1交于点A(2,m).
x+1交于点A(2,m).(1)求k、m的值;
(2)已知点P(n,0),过点P作平行于 y 轴的直线,交直线y=
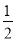 x+1于点B,交函数y=
x+1于点B,交函数y= (x>0)的图象于点C.若y=
(x>0)的图象于点C.若y= (x>0)的图象在点A、C之间的部分与线段AB、BC所围成的区域内(不包括边界),记作图形G.横、纵坐标都是整数的点叫做整点.
(x>0)的图象在点A、C之间的部分与线段AB、BC所围成的区域内(不包括边界),记作图形G.横、纵坐标都是整数的点叫做整点.①当n=4时,直接写出图形G的整点坐标;
②若图形G 恰有2 个整点,直接写出n的取值范围.
相关试题

