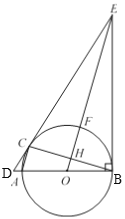
【题目】如图,AB是⊙O的直径,C 是⊙O上一点,过点C 作⊙O的切线,交BA的延长线交于点D,过点B 作BE⊥BA,交DC延长线于点E,连接OE,交⊙O于点F,交BC于点H,连接AC.
(1)求证:∠ECB=∠EBC;
(2)连接BF,CF,若BF=5,sin∠FBC=![]() ,求AC的长.
,求AC的长.
参考答案:
【答案】(1)见详解;(2)![]()
【解析】
(1)先证EB为⊙O的切线,再利用切线长定理即可证得∠ECB=∠EBC;
(2)先由BF=5,sin∠FBC=![]() 求得FH及HB的长,再由Rt△BOH的勾股定理求得OH长,最后利用中位线即可求得AC的长.
求得FH及HB的长,再由Rt△BOH的勾股定理求得OH长,最后利用中位线即可求得AC的长.
(1)证明:∵BE⊥BA,AB是⊙O的直径,
∴BE是⊙O的切线,
又∵CE是⊙O的切线,
∴BE=CE,
∴∠ECB=∠EBC;
(2)解:如图,连接OC,
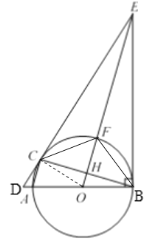
∵BE=CE,OB=OC,
∴OE垂直平分BC,
∴∠BHF=∠BHO=90°,点H为BC的中点,
∴在Rt△BHF中,sin∠FBC=![]() =
=![]() ,
,
∵BF=5,
∴FH=3,
∴BH=![]() ,
,
设OH=x,则OB=OF=x+3,
在Rt△OHB中,OH2+BH2=OB2,
∴x2+42=(x+3)2,
解得x=![]()
∴OH=![]()
∵点O、H分别为AB、CB的中点,
∴OH是△ABC的中位线,
∴AC=2OH=![]()
-
科目: 来源: 题型:
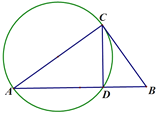
查看答案和解析>>【题目】下面是娜娜设计的“作一个角等于已知角”的尺规作图过程.
已知:RT△ABC,
求作:AB上作点D,使∠BCD=∠A.

作法:如图,以AC为直径作圆,交AB于D,所以点D就是所求作的点;
根据娜娜设计的作图过程,完成下面的证明.
证明:∵AC是直径
∴∠ADC=90°(______)(填推理的依据)
即∠ACD+∠A=90°,
∵∠ACB=90°,
即∠ACD+_______=90°,
∴∠BCD=∠A(_______)(填推理的依据).
-
科目: 来源: 题型:
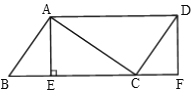
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AE⊥BC于E,点F在BC延长线上,且CF=BE,连接AC,DF,
(1)求证:四边形AEFD是矩形;
(2)若∠ACD=90°,CF=3,DF=4,求AD的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】央视举办的《主持人大赛》受到广泛的关注.某中学学生会就《主持人大赛》节目的喜爱程度,在校内对部分学生进行了问卷调查,并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级,分别记作
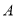 、
、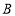 、
、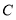 、
、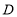 .根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中所给信息解答下列问题:
.根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中所给信息解答下列问题: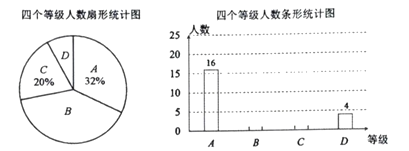
(1)本次被调查对象共有 人;扇形统计图中被调查者“比较喜欢”等级所对应圆心角的度数为 .
(2)将条形统计图补充完整,并标明数据;
(3)若选“不太喜欢”的人中有两个女生和两个男生,从选“不太喜欢”的人中挑选两个学生了解不太喜欢的原因,请用列举法(画树状图或列表),求所选取的这两名学生恰好是一男一女的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,函数y=
 (x>0)的图象与直线y=
(x>0)的图象与直线y=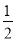 x+1交于点A(2,m).
x+1交于点A(2,m).(1)求k、m的值;
(2)已知点P(n,0),过点P作平行于 y 轴的直线,交直线y=
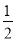 x+1于点B,交函数y=
x+1于点B,交函数y= (x>0)的图象于点C.若y=
(x>0)的图象于点C.若y= (x>0)的图象在点A、C之间的部分与线段AB、BC所围成的区域内(不包括边界),记作图形G.横、纵坐标都是整数的点叫做整点.
(x>0)的图象在点A、C之间的部分与线段AB、BC所围成的区域内(不包括边界),记作图形G.横、纵坐标都是整数的点叫做整点.①当n=4时,直接写出图形G的整点坐标;
②若图形G 恰有2 个整点,直接写出n的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在研究反比例函数
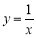 的图象与性质时,我们对函数解析式进行了深入分析.
的图象与性质时,我们对函数解析式进行了深入分析.首先,确定自变量
 的取值范围是全体非零实数,因此函数图象会被
的取值范围是全体非零实数,因此函数图象会被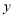 轴分成两部分;其次,分析解析式,得到
轴分成两部分;其次,分析解析式,得到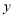 随
随 的变化趋势:当
的变化趋势:当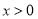 时,随着
时,随着 值的增大,
值的增大,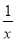 的值减小,且逐渐接近于零,随着
的值减小,且逐渐接近于零,随着 值的减小,
值的减小,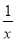 的值会越来越大…,由此,可以大致画出
的值会越来越大…,由此,可以大致画出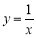 在
在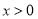 时的部分图象,如图所示:
时的部分图象,如图所示: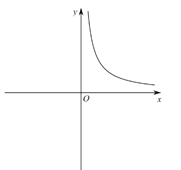
利用同样的方法,我们可以研究函数
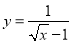 的图象与性质.通过分析解析式画出部分函数图象如图所示.
的图象与性质.通过分析解析式画出部分函数图象如图所示.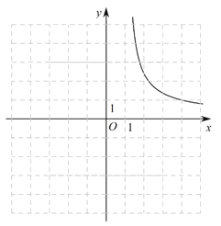
(1)请沿此思路在图中完善函数图象的草图并标出此函数图象上横坐标为0的点
 ;(画出网格区域内的部分即可)
;(画出网格区域内的部分即可)(2)观察图象,写出该函数的一条性质:__________;
(3)若关于
 的方程
的方程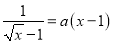 有两个不相等的实数根,结合图象,直接写出实数
有两个不相等的实数根,结合图象,直接写出实数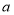 的取值范围: __________.
的取值范围: __________. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=ax22a2x(a
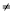 0)的对称轴与x轴交于点P.
0)的对称轴与x轴交于点P.(1)求点P的坐标(用含a的代数式表示);
(2)记函数y=x+2(1
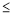 x
x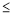 2)的图象为图形M,若抛物线与图形M恰有一个公共点,结合函数的图象,求a的取值范围.
2)的图象为图形M,若抛物线与图形M恰有一个公共点,结合函数的图象,求a的取值范围.
相关试题

