【题目】如图,四边形ABCD中,∠ABC=∠ADC=90°,BD⊥AC,垂足为P. 
(1)请作出Rt△ABC的外接圆⊙O;(保留作图痕迹,不写作法)
(2)点D在⊙O上吗?说明理由;
(3)试说明:AC平分∠BAD.
参考答案:
【答案】
(1)解:如图,⊙O为所作;
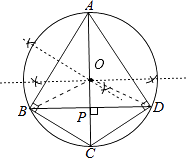
(2)解:点D在⊙O上.理由如下:
连结OD,

∵∠ABC=90°,
∴AC是⊙O的直径,
∵∠ADB=90°,
∴OD= ![]() AC,即OD=OA,
AC,即OD=OA,
∴点D在⊙O上
(3)解:∵AC是⊙O的直径,BD⊥AC,
∴BC=CD,
∴ ![]()
∴∠BAC=∠DAC,
∴AC平分∠BAD
【解析】(1)作AB和BC的垂直平分线,两垂直平分线相交于点O,以OB为半径作⊙O即可;(2)连结OD,先判断AC是⊙O的直径,而∠ADB=90°,根据直角三角形斜边上的中线性质得OD= ![]() AC,即OD=OA,于是根据点与圆的位置关系可判断点D在⊙O上;(3)由于AC是⊙O的直径,BD⊥AC,根据垂径定理得BC=CD,则
AC,即OD=OA,于是根据点与圆的位置关系可判断点D在⊙O上;(3)由于AC是⊙O的直径,BD⊥AC,根据垂径定理得BC=CD,则 ![]() ,然后根据圆周角定理可得∠BAC=∠DAC.
,然后根据圆周角定理可得∠BAC=∠DAC.
【考点精析】认真审题,首先需要了解三角形的外接圆与外心(过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心).
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)2x2﹣x=1
(2)x2+4x+2=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣6,0),B(﹣1,1),C(﹣3,3),将△ABC绕点B顺时针方向旋转90°后得到△A1BC1 .
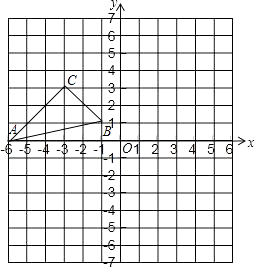
(1)画出△A1BC1 , 写出点A1、C1的坐标;
(2)计算线段BA扫过的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色不同外,其它都一样),其中红球2个,蓝球1个,现在从中任意摸出一个红球的概率为
 .
.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法求两次摸出的都是红球的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数与反比例函数y=
 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点. 
(1)求反比例函数的解析式;
(2)点P是x轴上的一动点,试确定点P使PA+PB最小,并求出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程:x2﹣2(m+1)x+m2+5=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若原方程的两个实数根为x1、x2 , 且满足x12+x22=|x1|+|x2|+2x1x2 , 求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于点D,过点D作DE∥BC交AC的延长线于点E.
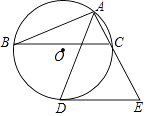
(1)试判断DE与⊙O的位置关系,并证明你的结论;
(2)若∠E=60°,⊙O的半径为5,求AB的长.
相关试题

