Question

【题目】如图，△ABC内接于⊙O，AD平分∠BAC交⊙O于点D，过点D作DE∥BC交AC的延长线于点E．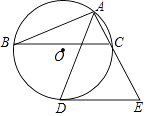
（1）试判断DE与⊙O的位置关系，并证明你的结论；
（2）若∠E=60°，⊙O的半径为5，求AB的长．

Answer 1

【答案】
（1）解：DE与⊙O相切，

理由：连接DO并延长到圆上一点N，交BC于点F，

∵AD平分∠BAC交⊙O于点D，

∴∠BAD=∠DAC，

∴ ，

∴DO⊥BC，

∵DE∥BC，

∴∠EDO=90°，

∴DE与⊙O相切

（2）解：连接AO并延长到圆上一点M，连接BM，

∵BC∥DE，

∴∠ACB=∠E=60°，

∴∠M=60°，

∵⊙O的半径为5，

∴AM=10，

∴BM=5，则AB= =5 ．

【解析】（1）利用垂径定理的推论结合平行线的性质得出∠EDO=90°，进而得出答案；（2）结合已知利用圆周角定理以及勾股定理得出AB的长．