【题目】如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点(且点P不与点B、C重合),PE⊥AB于E,PF⊥AC于F,M为EF中点.设AM的长为x,则x的取值范围是( )

A. 4≥x>2.4 B. 4≥x≥2.4 C. 4>x>2.4 D. 4>x≥2.4
参考答案:
【答案】D
【解析】
根据勾股定理的逆定理求出△ABC是直角三角形,得出四边形AEPF是矩形,求出AM=![]() EF=
EF=![]() AP,求出AP≥4.8,即可得出答案.
AP,求出AP≥4.8,即可得出答案.

解:连接AP.
∵AB=6,AC=8,BC=10,
∴AB2+AC2=36+64=100,BC2=100,
∴AB2+AC2=BC2,
∴∠BAC=90°,
∵PE⊥AB,PF⊥AC,
∴∠AEP=∠AFP=∠BAC=90°,
∴四边形AEPF是矩形,
∴AP=EF,
∵∠BAC=90°,M为EF中点,
∴AM=![]() EF=
EF=![]() AP,
AP,
当AP⊥BC时,AP值最小,
此时S△BAC=![]() ×6×8=
×6×8=![]() ×10×AP,
×10×AP,
AP=4.8,
即AP的范围是AP≥4.8,
∴2AM≥4.8,
∴AM的范围是AM≥2.4(即x≥2.4).
∵P为边BC上一动点,当P和C重合时,AM=4,
∵P和B、C不重合,
∴x<4,
综上所述,x的取值范围是:2.4≤x<4.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )

A.12
B.15
C.16
D.18 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=
 BC,连接CD和EF.
BC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知EF//AD, ∠1=∠2, ∠BAC=70°.求∠AGD的度数(将以下过程填写完整)

解:∵EF//AD
∴∠2=
又∵∠1=∠2
∴∠1=∠3
∴ AB//
∴∠BAC+ =180°.
又∵∠BAC=70°
∴∠AGD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家商店要进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可完成,需付两组费用共3480元,问:
(1)甲、乙两组工作一天,商店应各付多少元?
(2)已知甲组单独做需12天完成,乙组单独做需24天完成,单独请哪组,商店所付费用最少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,点E是边DC上一点,连接AE交BC的延长线于点H,点F是边AB上一点,使得
,点E是边DC上一点,连接AE交BC的延长线于点H,点F是边AB上一点,使得 ,作
,作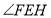 的角平分线
的角平分线 交BH于点G,若
交BH于点G,若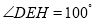 ,则
,则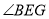 的度数是( )
的度数是( ) 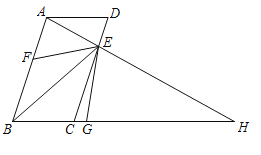
A.
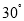 B.
B.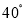 C.
C.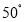 D.
D.
-
科目: 来源: 题型:
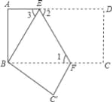
查看答案和解析>>【题目】如图,已知把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C′的位置上,若∠1=60°,AE=2.
(1)求∠2,∠3的度数.
(2)求长方形ABCD的纸片的面积S.
相关试题

