【题目】已知关于x的一元二次方程.（其中m为实数）

（1）若此方程的一个非零实数根为k，

① 当k = m时，求m的值；

② 若记为y，求y与m的关系式；

（2）当＜m＜2时，判断此方程的实数根的个数并说明理由

参考答案：

【答案】（1）

①1

②

（2）当＜m＜2时，此方程有两个不相等的实数根

【解析】解：（1）∵ k为的实数根，

∴.※ …………………………………………1分

① 当k = m时，

∵ k为非零实数根，

∴ m ≠ 0，方程※两边都除以m，得.

整理，得.

解得， . ………………………………………………………2分

∵是关于x的一元二次方程，

∴ m ≠ 2.

∴ m=" 1." ……………………………………………………………………3分

（阅卷说明：写对m= 1，但多出其他错误答案扣1分）

② ∵ k为原方程的非零实数根，

∴ 将方程※两边都除以k，得.…………………4分

整理，得.

∴.……………………………………………5分

（2）解法一： .………6分

当＜m＜2时，m＞0， ＜0.

∴＞0， ＞1＞0，Δ＞0.

∴ 当＜m＜2时，此方程有两个不相等的实数根. ……………7分

解法二：直接分析＜m＜2时，函数的图象，

∵ 该函数的图象为抛物线，开口向下，与y轴正半轴相交，

∴ 该抛物线必与x轴有两个不同交点. …………………………6分

∴ 当＜m＜2时，此方程有两个不相等的实数根. ……………7分

解法三： .…………6分

结合关于m的图象可知，（如图6）

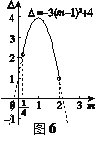
当＜m≤1时， ＜≤4；

当1＜m＜2时，1＜＜4.

∴ 当＜m＜2时， ＞0.

∴ 当＜m＜2时，此方程有两个不相等的实数根.…7分

关闭