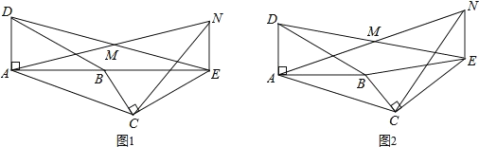
【题目】如图,已知△BAD≌△BCE,∠BAD=∠BCE=90°,∠ABD=∠BEC=30°,点 M 为 DE的中点,过点E与AD平行的直线交射线AM于点 N.
(1)如 图 1,当 A、B、E三点在同一直线上时,
①求证:△MEN≌△MDA;
②判断 AC与 CN数量关系为_______,并说明理由.
(2)将图 1 中△BCE绕 点 B 逆时针旋转一周,旋转过程中△CAN 能否为等腰直角三角形?若能,直接写出旋转角度;若不能,说明理由.
参考答案:
【答案】(1)①见解析,②AC=CN,见解析;(2)△BCE绕点B逆时针旋转一周,旋转过程中△CAN为等腰直角三角形时,旋转角度为60°或240°.
【解析】
(1)①先判断出BC=AD,EC=AB,再判断出∠MEN=∠MDA,即可得出结论;②首先证明△MEN≌△MDA,得BC=EN;然后证明△ABC≌△CEN,得到AC=CN;
(2)首先证明△MEN≌△MDA,得BC=EN;然后证明△ABC≌△CEN,得到AC=CN,再判断出∠ACB=90°,进而判断出∠BAC=∠ACB,再由BA≠CB,得出点A,B,C在同一条直线上,即可得出结论.
解:(1)①∵△BAD≌△BCE,
∴BC=AD,EC=AB.
∵EN∥AD,
∴∠MEN=∠MDA.
在△MEN与△MDA中,
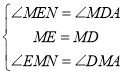
∴△MEN≌△MDA(ASA),
②AC=CN,
由①知,△MEN≌△MDA,
∴EN=AD,
∴EN=BC.
在△ABC与△CEN中,
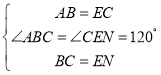
∴△ABC≌△CEN(SAS),
∴AC=CN.
(2)与(1)同理,可证明△MEN≌△MDA,
∴EN=BC.
设旋转角为α,则∠ABC=120°+α,
∠DBE=360°-∠DBA-∠ABC-∠CBE=360°-30°-(120°+α)-60°=150°-α.
∵BD=BE,
![]() ,
,
∵EN∥AD,
∴∠MEN=∠MDA=∠ADB+∠BDE=![]() ,
,
![]() ,
,
∴∠ABC=∠CEN.
在△ABC与△CEN中,
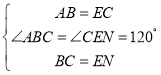 ,
,
∴△ABC≌△CEN(SAS),
∴AC=CN,∠BAC=∠NCE,
∵△CAN能成为等腰直角三角形
∴∠ACN=90°,
∴∠ACB=∠NCE,
∴∠BAC=∠ACB,
∵AB≠CB,
∴点A,B,C在同一条直线上,
此时旋转角为60°.如下图所示:
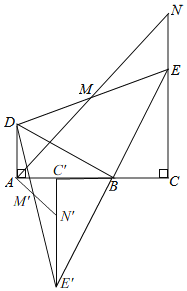
即△BCE绕点B逆时针旋转一周,旋转过程中△CAN为等腰直角三角形时,旋转角度为60°或240°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某课外活动小组为了了解本校学生上网目的,随机调查了本校的部分学生,根据调查结果,统计整理并制作了如下尚不完整的统计图,根据以上信息解答下列问题:
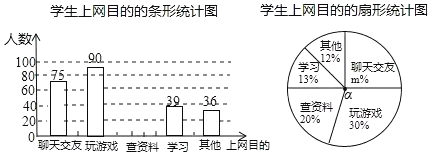
(1)参与本次调查的学生共有_____人;
(2)在扇形统计图中,m的值为_____;圆心角α=_____度.
(3)补全条形统计图;
(4)中学生上网玩游戏、聊天交友已经对正常的学习产生较多负面影响,为此学校计划开展一次“合理上网”专题讲座,每班随机抽取15名学生参加,小明所在的班级有50名学生,他被抽到听讲座的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=( )

A. 4 B. 6 C. 8 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2;
②方程
 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
像
 、
、 、
、 ……两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.例如
……两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.例如 与
与 ,
, 与
与 ,
, 与
与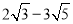 等都是互为有理化因式.
等都是互为有理化因式.在进行二次根式计算时,利用有理化因式,可以化去分母中的根号。
例如:
 ;
;
解答下列问题:
(1)
 与 互为有理化因式,将
与 互为有理化因式,将 分母有理化得
分母有理化得 (2)计算:

(3)观察下面的变形规律并解决问题:
①
 ,
, ,
, ,
, ……若
……若 为正整数,请你猜想
为正整数,请你猜想
②计算:

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.
(1) 求证:CP是⊙O的切线;
(2) 若PC=6,AB=4
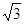 ,求图中阴影部分的面积.
,求图中阴影部分的面积.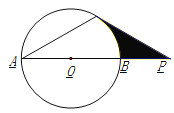
-
科目: 来源: 题型:
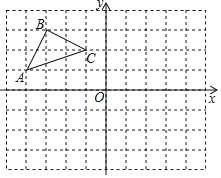
查看答案和解析>>【题目】按要求完成作图:
(1)作出△ABC关于x轴对称的图形;
(2)写出A、B、C的对应点A′、B′、C′的坐标;
(3)直接写出△ABC的面积 .
相关试题

