【题目】△ABC在平面直角坐标系中的位置如图所示,△ABC的顶点均在格点上,其中每个小正方形的边长为1个单位长度,将△ABC绕原点O旋转180°得△A1B1C1 . 
(1)在图中画出△A1B1C1;
(2)写出点A1的坐标;
(3)求出点C所经过的路径长.
参考答案:
【答案】
(1)解:如图所示,△A1B1C1即为所求;
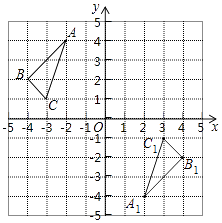
(2)(2,﹣4)
(3)解:由勾股定理可得,CO= ![]()
∴点C所经过的路径长为: ![]() ×2×π×
×2×π× ![]() =
= ![]() π.
π.
【解析】解:(1)如图所示,△A1B1C1即为所求;

(2)由图可得,点A1的坐标为(2,﹣4),
(3)由勾股定理可得,CO= 10
∴点C所经过的路径长为: ![]() ×2×π×
×2×π× ![]() =
= ![]() π.
π.
所以答案是:(1)见解答过程;(2)(2,﹣4);(3)![]() π.
π.
【考点精析】根据题目的已知条件,利用图形的旋转和旋转的性质的相关知识可以得到问题的答案,需要掌握每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】23.8°=______(化成度、分、秒的形式)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知□ABCD,AB∥x轴,AB=6,点A的坐标为(1,﹣4),点D的坐标为(﹣3,4),点B在第四象限,点P是□ABCD边上的一个动点.
(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x﹣1上,求点P的坐标.
(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标.(直接写出答案)
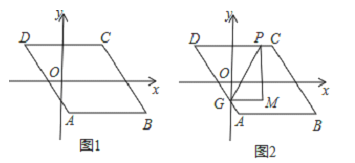
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2﹣2x+6的最小值是 .
-
科目: 来源: 题型:
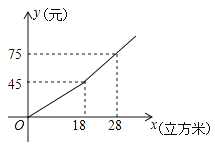
查看答案和解析>>【题目】某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准,该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.
(1)若某月用水量为18立方米,则应交水费多少元?
(2)求当x>18时,y关于x的函数表达式,若小敏家某月交水费81元,则这个月用水量为多少立方米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】位于环水东湾新城区的茂名市第一中学新校区占地面积约为536.5亩.将536.5用科学记数法可表示为( )
A.0.5365×103
B.5.365×102
C.53.65×10
D.536.5 -
科目: 来源: 题型:
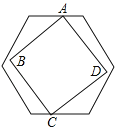
查看答案和解析>>【题目】如图,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是 .
相关试题

