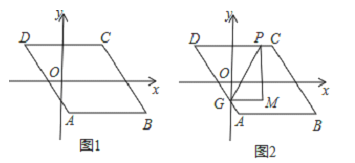
【题目】如图1,已知□ABCD,AB∥x轴,AB=6,点A的坐标为(1,﹣4),点D的坐标为(﹣3,4),点B在第四象限,点P是□ABCD边上的一个动点.
(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x﹣1上,求点P的坐标.
(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标.(直接写出答案)
参考答案:
【答案】(1)点P坐标为(3,4);(2)点P的坐标为(﹣3,4)或(﹣1,0)或(5,﹣4)或(3,﹣4);(3)点P坐标为(2,﹣4)或(﹣![]() ,3)或(﹣
,3)或(﹣![]() ,4)或(
,4)或(![]() ,4).
,4).
【解析】试题分析:(1)点P在BC上,要使PD=CD,只有P与C重合;
(2)首先要分点P在边AB,AD上时讨论,根据“点P关于坐标轴对称的点Q”,即还要细分“点P关于x轴的对称点Q和点P关于y轴的对称点Q”讨论,根据关于x轴、y轴对称点的特征(关于x轴对称时,点的横坐标不变,纵坐标变成相反数;关于y轴对称时,相反;)将得到的点Q的坐标代入直线y=x-1,即可解答;
(3)在不同边上,根据图象,点M翻折后,点M’落在x轴还是y轴,可运用相似求解.
试题解析:(1)∵CD=6,∴点P与点C重合,∴点P的坐标是(3,4).
(2)①当点P在边AD上时,由已知得,直线AD的函数表达式为:![]() ,设P(a,-2a-2),且-3≤a≤1.
,设P(a,-2a-2),且-3≤a≤1.
若点P关于x轴对称点Q1(a,2a+2)在直线y=x-1上,∴2a+2=a-1,解得a=-3,此时P(-3,4).
若点P关于y轴对称点Q2(-a,-2a-2)在直线y=x-1上,∴-2a-2=-a-1,解得a=-1,此时P(-1,0).
②当点P在边AB上时,设P(a,-4),且1≤a≤7.
若点P关于x轴对称点Q3(a,4)在直线y=x-1上,∴4=a-1,解得a=5,此时P(5,-4).
若点P关于y轴对称点Q4(-a,-4)在直线y=x-1上,∴-4=-a-1,解得a=3,此时P(3,-4).
综上所述,点P的坐标为(-3,4)或(-1,0)或(5,-4)或(3,-4).
(3)因为直线AD为y=-2x-2,所以G(0,-2).
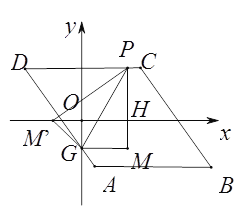
①如图,当点P在CD边上时,可设P(m,4),且-3≤m≤3,则可得M′P=PM=4+2=6,M′G=GM=|m|,易证得△OGM′∽△HM′P,则![]() ,即
,即![]() ,则OM′=
,则OM′=![]() ,在Rt△OGM′中,由勾股定理得,
,在Rt△OGM′中,由勾股定理得,![]() ,解得m=-
,解得m=-![]() 或
或![]() ,则P(-
,则P(-![]() ,4)或(
,4)或(![]() ,4);
,4);
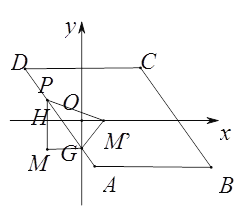
②如下图,当点P在AD边上时,设P(m,-2m-2),则PM′=PM=|-2m|,GM′=MG=|m|,易证得△OGM′∽△HM′P,则![]() ,即
,即![]() ,则OM′=
,则OM′=![]() ,在Rt△OGM′中,由勾股定理得,
,在Rt△OGM′中,由勾股定理得,![]() ,整理得m= -
,整理得m= -![]() ,则P(-
,则P(-![]() ,3);
,3);
如下图,当点P在AB边上时,设P(m,-4),此时M′在y轴上,则四边形PM′GM是正方形,所以GM=PM=4-2=2,则P(2,-4).
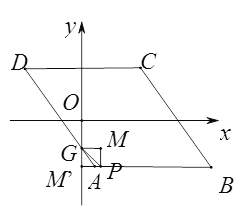
综上所述,点P的坐标为(2,-4)或(-![]() ,3)或(-
,3)或(-![]() ,4)或(
,4)或(![]() ,4).
,4).
-
科目: 来源: 题型:
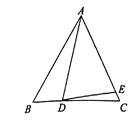
查看答案和解析>>【题目】已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE ,设∠BAD=α,∠CDE=β.
(1)如图,若点D在线段BC上,点E在线段AC上.
①如果∠ABC=60°,∠ADE=70°, 那么α=_______,β=_______.
②求α、β之间的关系式.
(2)是否存在不同于以上②中的α、β之间的关系式?若存在,求出这个关系式,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长度为50m .设饲养室为长为x(m),占地面积为
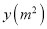 .
.(1)如图
 ,问饲养室为长x为多少时,占地面积y 最大?
,问饲养室为长x为多少时,占地面积y 最大?(2)如图
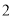 ,现要求在图中所示位置留2m的门,且仍使饲养室占地面积最大.小敏说:“只要饲养室长比(1)中的长多2m就行了.”请你通过计算,判断小敏的说法是否正确.
,现要求在图中所示位置留2m的门,且仍使饲养室占地面积最大.小敏说:“只要饲养室长比(1)中的长多2m就行了.”请你通过计算,判断小敏的说法是否正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】23.8°=______(化成度、分、秒的形式)
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2﹣2x+6的最小值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示,△ABC的顶点均在格点上,其中每个小正方形的边长为1个单位长度,将△ABC绕原点O旋转180°得△A1B1C1 .

(1)在图中画出△A1B1C1;
(2)写出点A1的坐标;
(3)求出点C所经过的路径长. -
科目: 来源: 题型:
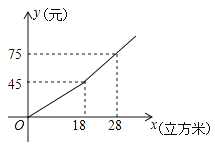
查看答案和解析>>【题目】某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准,该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.
(1)若某月用水量为18立方米,则应交水费多少元?
(2)求当x>18时,y关于x的函数表达式,若小敏家某月交水费81元,则这个月用水量为多少立方米?
相关试题

