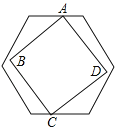
【题目】如图,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是 .
参考答案:
【答案】![]() ≤a≤
≤a≤![]() .
.
【解析】
试题分析:①当正方形ABCD的对角线AC在正六边形一组平行的对边的中点上时,正方形边长a的值最小,AC是正方形的对角线,∴AC=A′D=![]() ,∴a=
,∴a=![]() ;
;
②当正方形ABCD的四个顶点都在正六边形的边上时,正方形边长a的值最大,AC是正方形的对角线AC,则△AEB是等腰三角形,四边形AFGD是等腰梯形,过F,G分别作FH⊥AD,GN⊥AD,设AE=x,则AF=1﹣x,∴AB=![]() x,AH=DN=
x,AH=DN=![]() (1﹣x),∴AD=1+(1﹣x),∴
(1﹣x),∴AD=1+(1﹣x),∴![]() x=1+(1﹣x),∴x=
x=1+(1﹣x),∴x=![]() ,∴AB=
,∴AB=![]() ,∴正方形边长a的取值范围是:
,∴正方形边长a的取值范围是:![]() ≤a≤
≤a≤![]() ,故答案为:
,故答案为:![]() ≤a≤
≤a≤![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示,△ABC的顶点均在格点上,其中每个小正方形的边长为1个单位长度,将△ABC绕原点O旋转180°得△A1B1C1 .

(1)在图中画出△A1B1C1;
(2)写出点A1的坐标;
(3)求出点C所经过的路径长. -
科目: 来源: 题型:
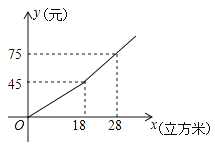
查看答案和解析>>【题目】某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准,该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.
(1)若某月用水量为18立方米,则应交水费多少元?
(2)求当x>18时,y关于x的函数表达式,若小敏家某月交水费81元,则这个月用水量为多少立方米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】位于环水东湾新城区的茂名市第一中学新校区占地面积约为536.5亩.将536.5用科学记数法可表示为( )
A.0.5365×103
B.5.365×102
C.53.65×10
D.536.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是( )
A.6
B.7
C.8
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司的年销售额为a元,成本为销售额的60%,税额和其他费用合计为销售额的P%.
(1)用关于a、P的代数式表示该公司的年利润;
(2)若a=8000万,P=7,则该公司的年利润为多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 一个有理数的平方根有两个,它们互为相反数
B. 一个有理数的立方根,不是正数就是负数
C. 负数没有立方根
D. 如果一个数的立方根是这个数本身,那么这个数一定是-1,0,1
相关试题

