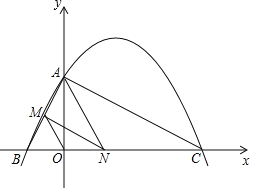
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.
参考答案:
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)N(3,0);(3)OM=
x+4;(2)N(3,0);(3)OM=![]() AC.
AC.
【解析】
试题分析:(1)由B、C的坐标,利用待定系数法可求得抛物线解析式;
(2)可设N(n,0),则可用n表示出△ABN的面积,由NM∥AC,可求得![]() ,则可用n表示出△AMN的面积,再利用二次函数的性质可求得其面积最大时n的值,即可求得N点的坐标;
,则可用n表示出△AMN的面积,再利用二次函数的性质可求得其面积最大时n的值,即可求得N点的坐标;
(3)由N点坐标可求得M点为AB的中点,由直角三角形的性质可得OM=![]() AB,在Rt△AOB和Rt△AOC中,可分别求得AB和AC的长,可求得AB与AC的关系,从而可得到OM和AC的数量关系.
AB,在Rt△AOB和Rt△AOC中,可分别求得AB和AC的长,可求得AB与AC的关系,从而可得到OM和AC的数量关系.
试题解析:(1)将点B,点C的坐标分别代入y=ax2+bx+4可得
![]() ,
,
解得 ,
,
∴二次函数的表达式为y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)设点N的坐标为(n,0)(﹣2<n<8),
则BN=n+2,CN=8﹣n.
∵B(﹣2,0),C(8,0),
∴BC=10,
在y=﹣![]() x2+
x2+![]() x+4中,令x=0,可解得y=4,
x+4中,令x=0,可解得y=4,
∴点A(0,4),OA=4,
∴S△ABN=![]() BNOA=
BNOA=![]() (n+2)×4=2(n+2),
(n+2)×4=2(n+2),
∵MN∥AC,
∴![]()
∴![]() ,
,
∴![]()
∵﹣![]() <0,
<0,
∴当n=3时,即N(3,0)时,△AMN的面积最大;
(3)当N(3,0)时,N为BC边中点,
∵MN∥AC,
∴M为AB边中点,
∴OM=![]() AB,
AB,
∵AB=![]() ,AC=
,AC=![]() ,
,
∴AB=![]() AC,
AC,
∴OM=![]() AC.
AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个三角形的两边长分别为4cm和7cm,那么第三边的长可能是( )
A.1cmB.4cmC.2cmD.3cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了扶持农民发展农业生产,国家对购买农机的农户给予农机售价13%的政府补贴.某市农机公司筹集到资金130万元,用于一次性购进A,B两种型号的收割机30台.根据市场需求,这些收割机可以全部销售,全部销售后利润不少于15万元.其中,收割机的进价和售价见下表:
A型收割机
B型收割机
进价(万元/台)
5.3
3.6
售价(万元/台)
6
4
设公司计划购进A型收割机x台,收割机全部销售后公司获得的利润为y万元.
(1)试写出y与x的函数关系式;
(2)市农机公司有哪几种购进收割机的方案可供选择?
(3)选择哪种购进收割机的方案,农机公司获利最大?最大利润是多少?此种情况下,购买这30台收割机的所有农户获得的政府补贴总额W为多少万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. a2a3=a6 B. (a2)3=a5
C. 2a2+3a2=5a6 D. (-2a)3=-8a3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形ABCD的边长为6cm,点F从点B出发,沿射线AB方向以1cm/秒的速度移动,点E从点D出发,向点A以1cm/秒的速度移动(不到点A).设点E,F同时出发移动t秒.
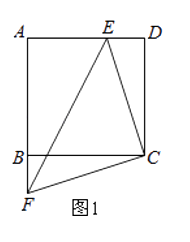
(1)在点E,F移动过程中,连接CE,CF,EF,则△CEF的形状是 , 始终保持不变;
(2)如图2,连接EF,设EF交BD移动M,当t=2时,求AM的长;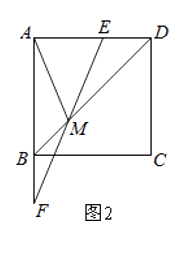
(3)如图3,点G,H分别在边AB,CD上,且GH=3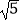 cm,连接EF,当EF与GH的夹角为45°,求t的值.
cm,连接EF,当EF与GH的夹角为45°,求t的值.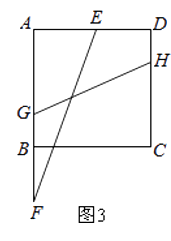
-
科目: 来源: 题型:
查看答案和解析>>【题目】跳绳比赛中以跳160个为标准,多跳或少跳的个数分别用正数与负数表示,如多跳了20个记作“+20”,那么“﹣8”表示 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面四个结论中,正确的是( )
A.三角形的三个内角中最多有一个锐角
B.等腰三角形的底角一定大于顶角
C.钝角三角形最多有一个锐角
D.三角形的三条内角平分线都在三角形内部
相关试题

