【题目】为了扶持农民发展农业生产,国家对购买农机的农户给予农机售价13%的政府补贴.某市农机公司筹集到资金130万元,用于一次性购进A,B两种型号的收割机30台.根据市场需求,这些收割机可以全部销售,全部销售后利润不少于15万元.其中,收割机的进价和售价见下表:
A型收割机 | B型收割机 | |
进价(万元/台) | 5.3 | 3.6 |
售价(万元/台) | 6 | 4 |
设公司计划购进A型收割机x台,收割机全部销售后公司获得的利润为y万元.
(1)试写出y与x的函数关系式;
(2)市农机公司有哪几种购进收割机的方案可供选择?
(3)选择哪种购进收割机的方案,农机公司获利最大?最大利润是多少?此种情况下,购买这30台收割机的所有农户获得的政府补贴总额W为多少万元?
参考答案:
【答案】
(1)解:y=(6﹣5.3)x+(4﹣3.6)(30﹣x)=0.3x+12
(2)解:依题意,有 
即  ∴
∴ ![]()
∵x为整数,∴x=10,11,12,
即农机公司有三种购进收割机的方案可供选择:
方案1:购进A型收割机10台,购进B型收割机20台;
方案2:购A型收割机11台,购B型收割机19台;
方案3:购进A型收割机12台,购B型收割机18台.
(3)解:∵0.3>0,
∴一次函数y随x的增大而增大.
即当x=12时,y有最大值,y最大值=0.3×12+12=15.6(万元),
此时,W=6×13%×12+4×13%×18=18.72(万元).
答:选择第三种方案获利最大,最大利润为15.6万元,获得的政府补贴为18.72万元
【解析】(1)y=(A型收割机售价﹣A型收割机进价)x+(B型收割机售价﹣B型收割机进价)×(30﹣x);(2)购买收割机总台数为30台,用于购买收割机的总资金为130万元,总的销售后利润不少于15万元.可得到两个一元一次不等式.(3)利用y与x的函数关系式y=0.3x+12来求最大利润.
【考点精析】解答此题的关键在于理解一元一次不等式组的应用的相关知识,掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果|a|>0,则a( )
A.一定是正数
B.一定是负数
C.一定不是负数
D.不等于0 -
科目: 来源: 题型:
查看答案和解析>>【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离约为多少米?(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个三角形的两边长分别为4cm和7cm,那么第三边的长可能是( )
A.1cmB.4cmC.2cmD.3cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. a2a3=a6 B. (a2)3=a5
C. 2a2+3a2=5a6 D. (-2a)3=-8a3
-
科目: 来源: 题型:
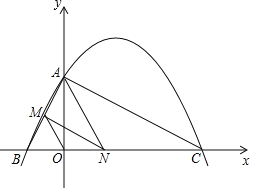
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形ABCD的边长为6cm,点F从点B出发,沿射线AB方向以1cm/秒的速度移动,点E从点D出发,向点A以1cm/秒的速度移动(不到点A).设点E,F同时出发移动t秒.
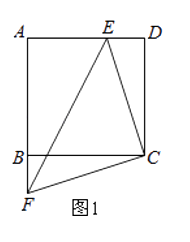
(1)在点E,F移动过程中,连接CE,CF,EF,则△CEF的形状是 , 始终保持不变;
(2)如图2,连接EF,设EF交BD移动M,当t=2时,求AM的长;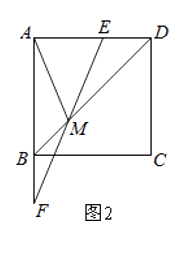
(3)如图3,点G,H分别在边AB,CD上,且GH=3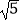 cm,连接EF,当EF与GH的夹角为45°,求t的值.
cm,连接EF,当EF与GH的夹角为45°,求t的值.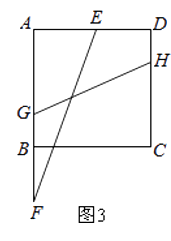
相关试题

