【题目】如图,在平面直角坐标系中,点0是坐标原点.边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,点E是对角线AC上一点,连接OE、BE,BE的延长线交OA于点P,若△OCE的面积为12.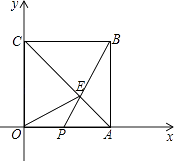
(1)求点E的坐标:
(2)求△OPE的周长.
参考答案:
【答案】
(1)解:过点E作EM⊥y轴于点M,
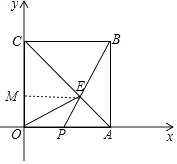
则 ![]() OCEM=12,
OCEM=12,
即 ![]() ×6×EM=12,
×6×EM=12,
∴EM=4,
∵四边形OABC是正方形,
∴∠MCE=45°,
∴△MEC是等腰直角三角形,
∴MC=ME=4,
∴MO=6﹣4=2,
∴点E的坐标是(4,2);
(2)解:设直线BE的解析式为y=kx+b,
把B(6,6)和点E(4,2)的坐标代入函数解析式得: ![]()
解得:k=2,b=﹣6,
∴直线BE的解析式为y=2x﹣6,
令2x﹣6=0得:x=3,
∴点P的坐标为(3,0),
∴OP=3,
∵四边形ABCO是正方形,
∴OC=CB,∠BCE=∠OCE,
在△OCE和△BCE中
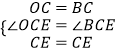
∴△OCE≌△BCE(SAS),
∴OE=BE,
在Rt△PBA中,由勾股定理可得:PB= ![]() =3
=3 ![]() ,
,
∴△OPE的周长=OE+PE+OP=3+PB=3+3 ![]() .
.
【解析】(1)题中已知△OCE的面积为12.因此过点E作EM⊥y轴于点M,利用三角形面积公式可求出ME的长,再证明△CME是等腰直角三角形,就可求出OM的长,即可求出点E的坐标。
(2)根据已知求出点B的坐标,利用待定系数法求出直线BE的解析式,再求出点P的坐标,即可求出OP的长,再证明△OCE≌△BCE,得到OE=BE,因此△OPE的周长就等于OP+BP,利用勾股定理求出PB的长,即可求得此三角形的周长。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 .
.(1)如图1,直接写出
 的数量关系为 ;
的数量关系为 ;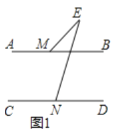
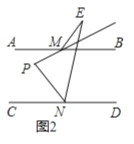
(2)如图2,
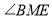 与
与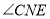 的角平分线所在的直线相交于点
的角平分线所在的直线相交于点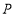 ,试探究
,试探究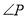 与
与 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中:
①由3x=﹣4系数化为1得x=﹣
 ;
;②由5=2﹣x移项得x=5﹣2;
③由
 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);④由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1.
其中正确的个数有( )
A. 0个 B. 1个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a=b,下列变形正确的有( )个.
①a+c=b+c;②a﹣c=b﹣c;③3a=3b;④ac=bc;⑤
 .
.A. 5 B. 4 C. 3 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4
 ,则S阴影=( )
,则S阴影=( ) 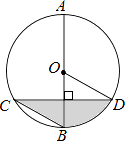
A.2π
B. π
π
C. π
π
D. π
π -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)2(10﹣0.5y)=﹣(1.5y+2)
(2)
 (x﹣5)=3﹣
(x﹣5)=3﹣ (x﹣5)
(x﹣5)(3)
 ﹣1=
﹣1=
(4)x﹣
 (x﹣9)=
(x﹣9)= [x+
[x+ (x﹣9)]
(x﹣9)](5)
 -
- =0.5x+2
=0.5x+2
相关试题

