【题目】如图,等边![]() 的边长为
的边长为![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 运动,点
运动,点![]() 从点
从点![]() 出发沿
出发沿![]() 的延长线
的延长线![]() 向右运动,已知点
向右运动,已知点![]() ,
,![]() 都以
都以![]() 的速度同时开始运动,运动过程中
的速度同时开始运动,运动过程中![]() 与
与![]() 相交于点
相交于点![]() ,点
,点![]() 运动到点
运动到点![]() 后两点同时停止运动.
后两点同时停止运动.
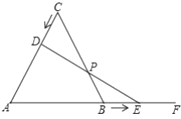
(1)当![]() 是直角三角形时,求
是直角三角形时,求![]() ,
,![]() 两点运动的时间;
两点运动的时间;
(2)求证:在运动过程中,点![]() 始终是线段
始终是线段![]() 的中点.
的中点.
参考答案:
【答案】(1)![]() 秒;(2)证明见解析
秒;(2)证明见解析
【解析】
(1)经过分析当△ADE是直角三角形时,只有∠ADE=90°的情况,此时∠AED=30°.用运动时间t表示出AD和AE,根据30度直角三角形的性质构造关于t的方程即可求解;
(2)过D点作DK∥AB交BC于点K,证明△DKP≌△EBP即可说明点P始终是线段DE的中点.
解:(1)![]() 中,
中,![]() ,
,![]()
所以若![]() 是直角三角形,只能
是直角三角形,只能![]()
![]() 中,
中,![]() 得,∠AED=30°
得,∠AED=30°
∴![]()
设![]() 点运动时间为
点运动时间为![]() ,则
,则![]() 点运动时间也为
点运动时间也为![]() .
.
∴![]() ,
,![]()
∴![]() ,解得
,解得![]()
所以当![]() 是直角三角形时,
是直角三角形时,![]() ,
,![]() 两点运动时间为
两点运动时间为![]() 秒.
秒.
(2)过点![]() 作
作![]() 交
交![]() 于点
于点![]()
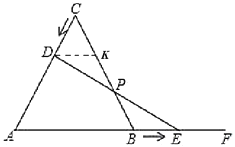
∵等边三角形![]() 中.
中.![]() ,
,![]()
且![]()
∴![]()
∴![]() 为等边三角形
为等边三角形
∴![]() ,
,![]()
设![]() ,
,![]() 运动时间为
运动时间为![]() 秒,则
秒,则![]()
在![]() 与
与![]() 中
中

∴![]()
∴![]()
∴![]() 始终为
始终为![]() 的中点
的中点
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司投资新建了一商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.每间的年租金每增加5 000元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5 000元.
(1)当每间商铺的年租金定为13万元时,能租出多少间?
(2)当每间商铺的年租金定为多少万元时,该公司的年收益(收益=租金-各种费用)为284万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两座仓库分别有农用车12辆和6辆.现在需要调往
 县10辆,需要调往
县10辆,需要调往 县8辆,已知从甲仓库调运一辆农用车到
县8辆,已知从甲仓库调运一辆农用车到 县和
县和 县的运费分别为40元和80元;从乙仓库调运一辆农用车到
县的运费分别为40元和80元;从乙仓库调运一辆农用车到 县和
县和 县的运费分别为30元和50元.
县的运费分别为30元和50元.(1)设乙仓库调往
 县农用车
县农用车 辆,求总运费
辆,求总运费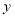 关于
关于 的函数关系式;
的函数关系式;(2)若要求总运费不超过900元,问共有几种调运方案?试列举出来.
(3)求出总运费最低的调运方案,最低运费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知AB=AC=6,BC=9,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.
(1)求证:△ABE∽△ECM;
(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由;

-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,
, ,点
,点 是
是 的中点,
的中点,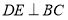 ,垂足为点
,垂足为点 ,连接
,连接 .
.(1)如图1,
 与
与 的数量关系是________;
的数量关系是________;
(2)如图2,若
 是线段
是线段 上一动点(点
上一动点(点 不与点
不与点 、
、 重合),连接
重合),连接 ,将线段
,将线段 绕点
绕点 逆时针旋转
逆时针旋转 ,得到线段
,得到线段 ,连接
,连接 ,请猜想
,请猜想 、
、 、
、 三者之间的数量关系,并证明你的结论;
三者之间的数量关系,并证明你的结论;
(3)若点
 是线段
是线段 延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出
延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出 、
、 、
、 三者之间的数量关系.
三者之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由两个长为8,宽为4的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是( )

A.15B.16C.19D.20
相关试题

