【题目】如图,由两个长为8,宽为4的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是( )

A.15B.16C.19D.20
参考答案:
【答案】D
【解析】
首先根据图1,证明四边形ABCD是菱形;然后判断出菱形的一条对角线为矩形的对角线时,四边形ABCD的面积最大,如图2,设AB=BC=x,则BE=8x,利用勾股定理求出x的值,即可求出四边形ABCD面积的最大值是多少.
如图1,作AE⊥BC于E,AF⊥CD于F,
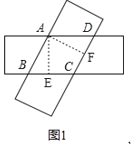
∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∵两个矩形的宽都是4,
∴AE=AF=4,
∵S四边形ABCD=AEBC=AFCD,
∴BC=CD,
∴平行四边形ABCD是菱形.
如图2,当菱形的一条对角线为矩形的对角线时,四边形ABCD的面积最大,
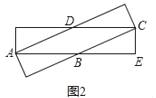
设AB=BC=x,则BE=8x,
∵BC2=BE2+CE2,
∴x2=(8x)2+42,
解得x=5,
∴四边形ABCD面积的最大值是:5×4=20.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边
 的边长为
的边长为 ,点
,点 从点
从点 出发沿
出发沿 向点
向点 运动,点
运动,点 从点
从点 出发沿
出发沿 的延长线
的延长线 向右运动,已知点
向右运动,已知点 ,
, 都以
都以 的速度同时开始运动,运动过程中
的速度同时开始运动,运动过程中 与
与 相交于点
相交于点 ,点
,点 运动到点
运动到点 后两点同时停止运动.
后两点同时停止运动.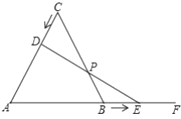
(1)当
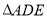 是直角三角形时,求
是直角三角形时,求 ,
, 两点运动的时间;
两点运动的时间;(2)求证:在运动过程中,点
 始终是线段
始终是线段 的中点.
的中点. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,
, ,点
,点 是
是 的中点,
的中点,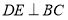 ,垂足为点
,垂足为点 ,连接
,连接 .
.(1)如图1,
 与
与 的数量关系是________;
的数量关系是________;
(2)如图2,若
 是线段
是线段 上一动点(点
上一动点(点 不与点
不与点 、
、 重合),连接
重合),连接 ,将线段
,将线段 绕点
绕点 逆时针旋转
逆时针旋转 ,得到线段
,得到线段 ,连接
,连接 ,请猜想
,请猜想 、
、 、
、 三者之间的数量关系,并证明你的结论;
三者之间的数量关系,并证明你的结论;
(3)若点
 是线段
是线段 延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出
延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出 、
、 、
、 三者之间的数量关系.
三者之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点
 是线段
是线段 的中点,过点
的中点,过点 作
作 的垂线
的垂线 ,在射线
,在射线 上有一个动点
上有一个动点 (点
(点 不与端点
不与端点 重合),连接
重合),连接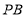 ,过点
,过点 作
作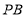 的垂线,垂足为点
的垂线,垂足为点 ,在射线
,在射线 上取点
上取点 ,使得
,使得 ,已知
,已知
(1)当
 时,求
时,求 的度数;
的度数;(2)过点
 作
作 垂直于直线
垂直于直线 交
交 于点
于点 ,在点
,在点 的运动过程中,
的运动过程中, 的大小随点
的大小随点 的运动而变化,在这个变化过程中线段
的运动而变化,在这个变化过程中线段 的长度是否发生变化?若不变,求出
的长度是否发生变化?若不变,求出 的长;若变化,请说明理由;
的长;若变化,请说明理由;(3)如图2,当
 时,设直线
时,设直线 与直线
与直线 相交于点
相交于点 ,求
,求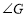 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,在等边△ABC中,点M是BC边上的任意一点(不含端点B,C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ACN=∠ABC.
【类比探究】
(2)如图②,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ACN=∠ABC还成立吗?请说明理由.
【拓展延伸】
(3)如图③,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】作图题
(1)如图①,点C是∠AOB边OB上的一点,在图中作出点C到OA的垂线段CD,垂足为D.再过C点作OA的平行线CE.
(2)如图②,在正方形网格中,每个小正方形的边长为1,△ABC的顶点都在正方形顶点上,将△ABC先向左平移2个单位,再向下平移3个单位,得到△A′B′C′,请你画出平移后的△A′B′C′.

相关试题

