【题目】如图,点B,F,C,E在一条直线上,AB=DE,AB∥DE,∠A=∠D.
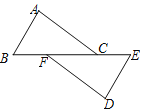
(1)求证:△ABC≌△DEF;(2)AC和DF存在怎样的关系?(直接写出答案)
参考答案:
【答案】(1)证明见解析;(2)AC=DF,AC∥DF.
【解析】
(1)根据两直线平行,内错角相等可得∠B=∠E,然后利用“角边角”证明△ABC和△DEF全等即可;
(2)根据全等三角形对应边相等可得AC=DF,对应角相等可得∠ACB=∠DFE,再利用内错角相等,两直线平行证明即可.
(1)∵AB∥DE,∴∠B=∠E.在△ABC和△DEF中,∵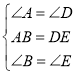 ,∴△ABC≌△DEF(ASA);
,∴△ABC≌△DEF(ASA);
(2)AC=DF,AC∥DF.理由如下:
∵△ABC≌△DEF,∴AC=DF,∠ACB=∠DFE,∴AC∥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
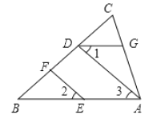
解:因为EF∥AD
所以∠2= ( )
又因为∠1=∠2
所以∠1=∠3( )
所以AB∥ ( )
所以∠BAC+ =180°( )
因为∠BAC=70°
所以∠AGD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(7分)如图所示,O是直线AB上一点,∠AOC=
 ∠BOC,OC是∠AOD的平分线.
∠BOC,OC是∠AOD的平分线.
(1)求∠COD的度数.
(2)判断OD与AB的位置关系,并说出理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中有一个黑球
 和两个白球
和两个白球 (除颜色外其他均相同).用树状图(或列表法)解答下列问题:
(除颜色外其他均相同).用树状图(或列表法)解答下列问题:(1)小丽第一次从袋子中摸出一个球不放回,第二次又从袋子中摸出一个球,则小丽两次都摸到白球的概率是多少?
(2)小强第一次从袋子中摸出一个球,摸到黑球不放回,摸到白球放回;第二次又从袋子中摸出一个球,则小强两次都摸到白球的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】 在△ABC中,AC=BC,∠ ACB=90°,AD平分∠BAC交BC边于点D,过B 作BH⊥AD,交AC的延长线于点E,H为垂足.
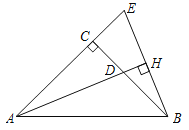
(1)求证: △ACD ≌ △BCE;
(2)找出BH和BC有怎样的数量关系(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,分别探讨下面四个图形中∠APC与∠A,∠C的关系,请你从所得的关系中任意选取一个加以说明.
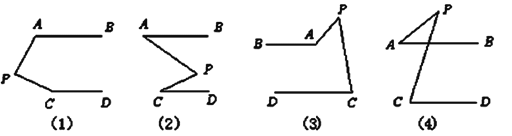
图(1)结论: ;图(2)结论: ;图(3)结论: ;图(4)结论: .
你准备证明的是图 ,请在下面写出证明过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,高
,高 ,
, 交于点
交于点 ,连接
,连接 并延长交
并延长交 于点
于点 ,则图中共有______________________组全等三角形.
,则图中共有______________________组全等三角形.
相关试题

