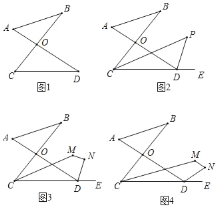
【题目】(1)如图1的图形我们把它称为“8字形”,则∠A,∠B,∠C,∠D四个角的数量关系是 ;
(2)如图2,若∠BCD,∠ADE的角平分线CP,DP交于点P,则∠P与∠A,∠B的数量关系为∠P= ;
(3)如图3,CM,DN分别平分∠BCD,∠ADE,当∠A+∠B=80°时,试求∠M+∠N的度数(提醒:解决此问题可以直接利用上述结论);
(4)如图4,如果∠MCD=![]() ∠BCD,∠NDE=
∠BCD,∠NDE=![]() ∠ADE,当∠A+∠B=n°时,试求∠M+∠N的度数.
∠ADE,当∠A+∠B=n°时,试求∠M+∠N的度数.
参考答案:
【答案】(1)∠A+∠B=∠C+∠D;(2)90°﹣![]() (∠A+∠B);(3)∠CMN+∠DNM=230°;(4)∠CMN+∠DNM=240°﹣
(∠A+∠B);(3)∠CMN+∠DNM=230°;(4)∠CMN+∠DNM=240°﹣![]() n°.
n°.
【解析】
(1)由三角形的内角和均为180°及图中∠AOB和∠COD为对顶角可知∠A+∠B=∠C+∠D;
(2)设∠PCD=x,∠ADP=y,由CP,DP均为角平分线可得∠BCD=2x,∠ADE=2y;再由三角形外角和定理可得∠P=∠PDE﹣∠PCD=y﹣x,∠COD=∠ODE﹣∠BCD=2y﹣2x,则可求得∠COD=2∠P;由三角形内角和定理以及∠COD和∠AOB是对顶角可得,∠COD+∠A+∠B=180°,再用∠COD=2∠P进行替换可得∠P=90°﹣![]() (∠A+∠B);
(∠A+∠B);
(3)延长CM、DN交于点P,由上一问结论可知∠P=90°﹣![]() (∠A+∠B),结合题干所给条件易求得∠P=50°,由三角形内角和定理可得∠PMN+∠PNM=130°,则∠M+∠N=360°-(∠PMN+∠PNM)=360°﹣130°=230°;
(∠A+∠B),结合题干所给条件易求得∠P=50°,由三角形内角和定理可得∠PMN+∠PNM=130°,则∠M+∠N=360°-(∠PMN+∠PNM)=360°﹣130°=230°;
(4)延长CM、DN交于点P,设∠PCD=x,∠ADP=2y,由∠MCD=![]() ∠BCD,∠NDE=
∠BCD,∠NDE=![]() ∠ADE易得∠NDE=y,∠BCD=3x,再由三角形外角和定理以及内角和定理易得∠P=y﹣x,∠COD=3y﹣3x,则∠COD=3∠P;由三角形内角和定理可得3∠P+∠A+∠B=180°,题干已知∠A+∠B=n°,则可知∠P=
∠ADE易得∠NDE=y,∠BCD=3x,再由三角形外角和定理以及内角和定理易得∠P=y﹣x,∠COD=3y﹣3x,则∠COD=3∠P;由三角形内角和定理可得3∠P+∠A+∠B=180°,题干已知∠A+∠B=n°,则可知∠P=![]() ,同上问∠CMN+∠DNM=360°﹣(∠PMN+∠PNM)=360°-(120°+
,同上问∠CMN+∠DNM=360°﹣(∠PMN+∠PNM)=360°-(120°+![]() )=240°﹣
)=240°﹣![]() .
.
解:(1)如图1,在△AOB中,∠A+∠B+∠AOB=180°,
在△COD中,∠C+∠D+∠COD=180°,
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
故答案为:∠A+∠B=∠C+∠D;
(2)设∠PCD=x,∠ADP=y,
∵CP,DP分别平分∠BCD,∠ADE,
∴∠BCD=2x,∠ADE=2y,
∵∠P=∠PDE﹣∠PCD=y﹣x,
∠COD=∠ODE﹣∠BCD=2y﹣2x,
∴∠COD=2∠P,
∵∠COD+∠A+∠B=180°,
∴2∠P+∠A+∠B=180°,
∴∠P=90°﹣![]() (∠A+∠B);
(∠A+∠B);
故答案为:90°﹣![]() (∠A+∠B);
(∠A+∠B);
(3)延长CM、DN交于点P,
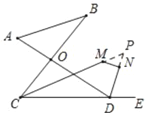
由(2)知:∠P=90°﹣![]() (∠A+∠B),
(∠A+∠B),
∵∠A+∠B=80°,
∴∠P=50°,
∴∠PMN+∠PNM=130°,
∴∠CMN+∠DNM=360°﹣130°=230°;
(4)延长CM、DN交于点P,

设∠PCD=x,∠ADP=2y,
∵∠MCD=![]() ∠BCD,∠NDE=
∠BCD,∠NDE=![]() ∠ADE,
∠ADE,
∴∠NDE=y,∠BCD=3x,
∴∠P=y﹣x,∠COD=3y﹣3x,
∴∠COD=3∠P,
∴3∠P+∠A+∠B=180°,
∵∠A+∠B=n°,
∴∠P=![]() ,
,
∴∠PMN+∠PNM=180°﹣![]() =120°+
=120°+![]() ,
,
∴∠CMN+∠DNM=360°﹣(120°+![]() )=240°﹣
)=240°﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 甲、乙两名学生在参加今年体育考试前各做了5次立定跳远测试,两人的平均成绩相同,其中甲所测得成绩的方差是0.005,乙所测得的成绩如下:2.20 m,2.30 m,2.30 m,2.40 m,2.30 m,那么甲、乙的成绩比较( )
A.甲的成绩更稳定B.乙的成绩更稳定
C.甲、乙的成绩一样稳定D.不能确定谁的成绩更稳定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD∥CO.
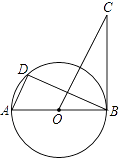
(1)求证:△ABD≌△OBC;
(2)若AB=2,BC=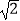 ,求AD的长.
,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形ABC中,∠C=90°,AD平分∠BAC交BC于点D,BE平分∠ABC交AC于点E,AD、BE相交于点F,过点D作DG∥AB,过点B作BG⊥DG交DG于点G.下列结论:①∠AFB=135°;②∠BDG=2∠CBE;③BC平分∠ABG;④∠BEC=∠FBG.其中正确的个数是( )

A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)

(1)求这条抛物线的解析式;
(2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出点Q的坐标;若不存在说明理由; -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
某商场用8万元购进一批新款衬衫,上架后很快销售一空,商场又紧急购进第二批这种衬衫,数量是第一次的2倍,但进价涨了4元/件,结果共用去17.6万元.
(1)该商场第一批购进衬衫多少件?
(2)商场销售这种衬衫时,每件定价都是58元,剩至150件时按八折出售,全部售完.售完这两批衬衫,商场共盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知PA、PB切⊙O于A,B两点,连AB,且PA,PB的长是方程x2﹣2mx+3=0的两根,AB=m.试求:
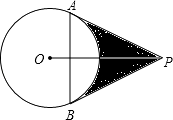
(1)⊙O的半径;
(2)由PA,PB, 围成图形(即阴影部分)的面积.
围成图形(即阴影部分)的面积.
相关试题

