【题目】如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD∥CO. 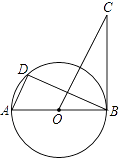
(1)求证:△ABD≌△OBC;
(2)若AB=2,BC= ![]() ,求AD的长.
,求AD的长.
参考答案:
【答案】
(1)证明:∵AB是⊙O的直径,
∴∠ADB=∠90°,
∵BC是⊙O的切线,
∴∠OBC=∠90°,
∵AD∥CO,
∴∠A=∠COB,
在△ABD和△OBC中
∵∠ADB=∠OBC,∠A=∠COB,
∴△ABD∽△OCB;
(2)解:由(1)知,△ABD∽△OCB,
∴ ![]() =
= ![]() ,即AD=
,即AD= ![]() ,
,
∵AB=2,BC= ![]() ,
,
∴OB=1,
∴OC= ![]() =
= ![]() ,
,
∴AD= ![]() =
= ![]() .
.
【解析】(1)根据AB为圆O的直径,根据圆周角定理得到∠D为90°,又BC为圆O的切线,根据切线性质得到∠CBO=90°,进而得到这两个角相等,又AD∥CO,根据两直线平行,得到一对同位角相等,从而利用两角对应相等的两三角形相似即可得证;(2)根据勾股定理求得OC= ![]() ,由(1)得到的相似三角形,根据相似三角形的对应边成比例得出
,由(1)得到的相似三角形,根据相似三角形的对应边成比例得出 ![]() =
= ![]() ,即AD=
,即AD= ![]() ,求出AD的长.
,求出AD的长.
【考点精析】通过灵活运用切线的性质定理,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是
 ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )A. 2,
 B. 2,1 C. 4,
B. 2,1 C. 4, D. 4,3
D. 4,3 -
科目: 来源: 题型:
查看答案和解析>>【题目】为缓解“停车难”的问题,某单位拟造地下停车库,建筑设计师提供了该地下停车库的设计示意图如图所示,已知该坡道的水平距离AB的长为9m,坡面AD与AB的夹角∠BAD=18°,石柱BC=0.5m,按规定,地下停车库坡道上方BC处要张贴限高标志,以便告知停车人车辆能否安全驶入.请你帮设计师计算一下CE的高度,以便张贴限高标志,结果精确到0.1m.
(参考数值:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
-
科目: 来源: 题型:
查看答案和解析>>【题目】 甲、乙两名学生在参加今年体育考试前各做了5次立定跳远测试,两人的平均成绩相同,其中甲所测得成绩的方差是0.005,乙所测得的成绩如下:2.20 m,2.30 m,2.30 m,2.40 m,2.30 m,那么甲、乙的成绩比较( )
A.甲的成绩更稳定B.乙的成绩更稳定
C.甲、乙的成绩一样稳定D.不能确定谁的成绩更稳定
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形ABC中,∠C=90°,AD平分∠BAC交BC于点D,BE平分∠ABC交AC于点E,AD、BE相交于点F,过点D作DG∥AB,过点B作BG⊥DG交DG于点G.下列结论:①∠AFB=135°;②∠BDG=2∠CBE;③BC平分∠ABG;④∠BEC=∠FBG.其中正确的个数是( )

A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1的图形我们把它称为“8字形”,则∠A,∠B,∠C,∠D四个角的数量关系是 ;
(2)如图2,若∠BCD,∠ADE的角平分线CP,DP交于点P,则∠P与∠A,∠B的数量关系为∠P= ;
(3)如图3,CM,DN分别平分∠BCD,∠ADE,当∠A+∠B=80°时,试求∠M+∠N的度数(提醒:解决此问题可以直接利用上述结论);
(4)如图4,如果∠MCD=
 ∠BCD,∠NDE=
∠BCD,∠NDE= ∠ADE,当∠A+∠B=n°时,试求∠M+∠N的度数.
∠ADE,当∠A+∠B=n°时,试求∠M+∠N的度数.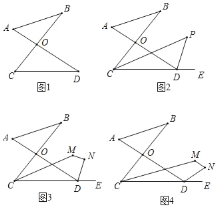
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)

(1)求这条抛物线的解析式;
(2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出点Q的坐标;若不存在说明理由;
相关试题

